📚 Class 11 Science and Commerce के Formulas 📚

Class 9 Class 10 Class 12 Competitive & Commerce

🔹 समुच्चय (Sets) के सूत्र 🔹

क्रमांक 🔢 व Formula 📖 + Explanation ✍️ + उदाहरण 🎯
1️⃣ रिक्त समुच्चय (∅) जिस समुच्चय में कोई तत्त्व नहीं होता। ∅ = { } (जैसे, ऐसा समुच्चय जिसमें कोई सदस्य न हो)
2️⃣ समुच्चय का पूरक (A') सभी तत्त्व जो सार्वभौमिक समुच्चय में हैं लेकिन A में नहीं। उदाहरण: यदि सार्वभौमिक समुच्चय U = {1,2,3,4,5} और A = {1,2}, तो A' = {3,4,5}
3️⃣ समुच्चयों का संघ (A ∪ B) सभी तत्त्व जो A या B या दोनों में हैं। उदाहरण: A = {1,2,3}, B = {3,4,5} तो A ∪ B = {1,2,3,4,5}
4️⃣ समुच्चयों का छेद (A ∩ B) सभी तत्त्व जो A और B दोनों में हैं। उदाहरण: A = {1,2,3}, B = {3,4,5} तो A ∩ B = {3}
5️⃣ समुच्चय अंतर (A - B) ऐसे तत्त्व जो A में हों लेकिन B में न हों। उदाहरण: A = {1,2,3}, B = {3,4,5} तो A - B = {1,2}
6️⃣ उपसमुच्चय (A ⊆ B) हर तत्त्व A का, B में भी हो। उदाहरण: यदि A = {1,2} और B = {1,2,3}, तो A ⊆ B
7️⃣ शक्ति समुच्चय (P(A)) सभी उपसमुच्चयों का समुच्चय। सूत्र: n(P(A)) = 2^n(A) उदाहरण: यदि A = {a,b} हो तो P(A) = {∅, {a}, {b}, {a,b}} और n(P(A)) = 2² = 4
8️⃣ दो समुच्चयों के संघ का सूत्र n(A ∪ B) = n(A) + n(B) - n(A ∩ B) उदाहरण: n(A) = 10, n(B) = 15, n(A ∩ B) = 5 तो n(A ∪ B) = 10 + 15 - 5 = 20
9️⃣ तीन समुच्चयों के संघ का सूत्र n(A ∪ B ∪ C) = n(A) + n(B) + n(C) - n(A ∩ B) - n(B ∩ C) - n(C ∩ A) + n(A ∩ B ∩ C) उदाहरण: यदि n(A) = 5, n(B) = 6, n(C) = 7, n(A ∩ B) = 2, n(B ∩ C) = 3, n(C ∩ A) = 2, n(A ∩ B ∩ C) = 1 हो, तो: n(A ∪ B ∪ C) = 5 + 6 + 7 - 2 - 3 - 2 + 1 = 12
🔟 डि मॉर्गन के नियम (A ∪ B)' = A' ∩ B' और (A ∩ B)' = A' ∪ B' उदाहरण: यदि सार्वभौमिक समुच्चय U = {1,2,3,4} और A = {1,2}, B = {2,3} हो, तो: (A ∪ B)' = {4} और (A ∩ B)' = {1,3,4}

क्रमांक 🔢 व Formula 📖 + Explanation ✍️ + उदाहरण 🎯

1️⃣ रिक्त समुच्चय (∅)

जिस समुच्चय में कोई तत्त्व नहीं होता।

∅ = { } (जैसे, ऐसा समुच्चय जिसमें कोई सदस्य न हो)

2️⃣ समुच्चय का पूरक (A')

सभी तत्त्व जो सार्वभौमिक समुच्चय में हैं लेकिन A में नहीं।

उदाहरण: यदि सार्वभौमिक समुच्चय U = {1,2,3,4,5} और A = {1,2}, तो A' = {3,4,5}

3️⃣ समुच्चयों का संघ (A ∪ B)

सभी तत्त्व जो A या B या दोनों में हैं।

उदाहरण: A = {1,2,3}, B = {3,4,5} तो A ∪ B = {1,2,3,4,5}

4️⃣ समुच्चयों का छेद (A ∩ B)

सभी तत्त्व जो A और B दोनों में हैं।

उदाहरण: A = {1,2,3}, B = {3,4,5} तो A ∩ B = {3}

5️⃣ समुच्चय अंतर (A - B)

ऐसे तत्त्व जो A में हों लेकिन B में न हों।

उदाहरण: A = {1,2,3}, B = {3,4,5} तो A - B = {1,2}

6️⃣ उपसमुच्चय (A ⊆ B)

हर तत्त्व A का, B में भी हो।

उदाहरण: यदि A = {1,2} और B = {1,2,3}, तो A ⊆ B

7️⃣ शक्ति समुच्चय (P(A))

सभी उपसमुच्चयों का समुच्चय।

सूत्र: n(P(A)) = 2^n(A)

उदाहरण: यदि A = {a,b} हो तो P(A) = {∅, {a}, {b}, {a,b}} और n(P(A)) = 2² = 4

8️⃣ दो समुच्चयों के संघ का सूत्र

n(A ∪ B) = n(A) + n(B) - n(A ∩ B)

उदाहरण: n(A) = 10, n(B) = 15, n(A ∩ B) = 5 तो n(A ∪ B) = 10 + 15 - 5 = 20

9️⃣ तीन समुच्चयों के संघ का सूत्र

n(A ∪ B ∪ C) = n(A) + n(B) + n(C) - n(A ∩ B) - n(B ∩ C) - n(C ∩ A) + n(A ∩ B ∩ C)

उदाहरण: यदि n(A) = 5, n(B) = 6, n(C) = 7, n(A ∩ B) = 2, n(B ∩ C) = 3, n(C ∩ A) = 2, n(A ∩ B ∩ C) = 1 हो, तो:

n(A ∪ B ∪ C) = 5 + 6 + 7 - 2 - 3 - 2 + 1 = 12

🔟 डि मॉर्गन के नियम

(A ∪ B)' = A' ∩ B' और (A ∩ B)' = A' ∪ B'

उदाहरण: यदि सार्वभौमिक समुच्चय U = {1,2,3,4} और A = {1,2}, B = {2,3} हो, तो:

(A ∪ B)' = {4} और (A ∩ B)' = {1,3,4}

🔹 समुच्चय (Sets) में उपयोग होने वाले प्रतीक (Symbols) 🔹

प्रतीक चिन्ह 🔤	नाम 📋
∪	संघ (Union)
∩	छेद (Intersection)
⊆	उपसमुच्चय (Subset)
⊂	उचित उपसमुच्चय (Proper Subset)
⊃	महासमुच्चय (Superset)
∅	रिक्त समुच्चय (Empty Set)
U	सार्वभौमिक समुच्चय (Universal Set)
'	पूरक (Complement)

🎯 उदाहरण (Examples) 🎯

🔹 उदाहरण 1: A = {1,2,3} और B = {3,4,5} तो:
- 👉 A ∪ B = {1,2,3,4,5}
- 👉 A ∩ B = {3}
- 👉 A - B = {1,2}
🔹 उदाहरण 2: सार्वभौमिक समुच्चय U = {1,2,3,4,5,6,7,8,9} और A = {2,4,6,8} हो तो:
- 👉 A' = {1,3,5,7,9}
🔹 उदाहरण 3: यदि n(A) = 10, n(B) = 15, और n(A ∩ B) = 5 हो, तो:
- 👉 n(A ∪ B) = 20
🔹 उदाहरण 4: यदि n(A) = 3 हो, तो शक्ति समुच्चय P(A) में:
- 👉 n(P(A)) = 2³ = 8

📚 बंध और फलन (Relation and Function) 📚

🔹 संबंध (Relation) के महत्वपूर्ण सूत्र 🔹

क्रमांक 🔢 व Formula 📖 + Explanation ✍️ + Example 🎯
1️⃣ संबंध (Relation) की परिभाषा यदि A और B दो गैर-रिक्त समुच्चय हैं, तो A × B = {(a,b) \| a ∈ A और b ∈ B} कहलाता है। 👉 उदाहरण 1: यदि A = {1,2} और B = {3,4} तो A × B ज्ञात कीजिए। Step 1: A के प्रत्येक तत्त्व को B के प्रत्येक तत्त्व से जोड़ना। Step 2: युग्म मिलेंगे: (1,3), (1,4), (2,3), (2,4) Step 3: अतः A × B = {(1,3), (1,4), (2,3), (2,4)}
2️⃣ परावर्ती संबंध (Reflexive Relation) यदि प्रत्येक a ∈ A के लिए (a,a) ∈ R हो, तो संबंध परावर्ती होता है। 👉 उदाहरण 2: A = {1,2} और R = {(1,1), (2,2)} है। जाँचिए कि R परावर्ती है या नहीं। Step 1: 1 के लिए (1,1) है ✅ और 2 के लिए (2,2) है ✅। Step 2: सभी तत्त्व स्वयं से जुड़े हैं। Step 3: अतः R परावर्ती संबंध है।
3️⃣ प्रत्यावर्ती संबंध (Symmetric Relation) यदि (a,b) ∈ R ⇒ (b,a) ∈ R, तो संबंध प्रत्यावर्ती होता है। 👉 उदाहरण 3: A = {1,2} और R = {(1,2), (2,1)} है। जाँचिए कि R प्रत्यावर्ती है या नहीं। Step 1: (1,2) है और उसके साथ (2,1) भी है ✅। Step 2: दोनों ओर समानता है। Step 3: अतः R प्रत्यावर्ती संबंध है।
4️⃣ पारगम्य संबंध (Transitive Relation) यदि (a,b) ∈ R और (b,c) ∈ R हो ⇒ (a,c) ∈ R, तो संबंध पारगम्य होता है। 👉 उदाहरण 4: A = {1,2,3} और R = {(1,2), (2,3), (1,3)} है। जाँचिए कि R पारगम्य है या नहीं। Step 1: (1,2) और (2,3) है ⇒ तो (1,3) होना चाहिए। Step 2: (1,3) है ✅। Step 3: अतः R पारगम्य संबंध है।
5️⃣ सार्वत्रिक संबंध (Universal Relation) यदि R = A × A हो, अर्थात् प्रत्येक संभव युग्म (a,b) ∈ R हो, तो संबंध सार्वत्रिक होता है। 👉 उदाहरण 5: A = {1,2} के लिए R = {(1,1), (1,2), (2,1), (2,2)} है। जाँचिए कि R सार्वत्रिक है या नहीं। Step 1: सभी संभव युग्म (1,1), (1,2), (2,1), (2,2) मौजूद हैं। Step 2: कोई भी युग्म छूटा नहीं है। Step 3: अतः R सार्वत्रिक संबंध है।
6️⃣ रिक्त संबंध (Empty Relation) यदि R = ∅ हो (कोई भी युग्म नहीं हो), तो संबंध रिक्त कहलाता है। 👉 उदाहरण 6: A = {1,2,3} और R = ∅ है। Step 1: R में कोई भी युग्म नहीं है। Step 2: कोई भी तत्त्व आपस में संबंधित नहीं है। Step 3: अतः यह रिक्त संबंध है।
7️⃣ एक-एक संबंध (One-One Relation) अगर प्रत्येक तत्त्व A का अलग-अलग तत्त्वों से B में मेल हो, तो उसे एक-एक संबंध कहते हैं। 👉 उदाहरण 7: A = {1,2,3}, B = {4,5,6} और R = {(1,4), (2,5), (3,6)} है। Step 1: 1 → 4, 2 → 5, 3 → 6। Step 2: कोई दो तत्त्व एक ही तत्त्व से नहीं जुड़े। Step 3: अतः यह एक-एक संबंध है।
8️⃣ कार्यात्मक संबंध (Functional Relation) अगर A का प्रत्येक तत्त्व B के केवल एक तत्त्व से जुड़ा हो, तो उसे कार्यात्मक संबंध कहते हैं। 👉 उदाहरण 8: A = {a,b} और B = {1,2,3}, R = {(a,2), (b,3)} है। Step 1: a केवल 2 से और b केवल 3 से जुड़ा है। Step 2: हर तत्त्व का एक ही output है। Step 3: अतः R एक कार्यात्मक संबंध है।
9️⃣ संक्रमणशील संबंध (Transitive Relation) यदि (a,b) ∈ R और (b,c) ∈ R हो, तो (a,c) ∈ R भी होना चाहिए, तब इसे संक्रमणशील संबंध कहते हैं। 👉 उदाहरण 9: A = {1,2,3} और R = {(1,2), (2,3), (1,3)} है। जाँचिए कि R संक्रमणशील है या नहीं। Step 1: (1,2) और (2,3) है ⇒ तो (1,3) होना चाहिए। Step 2: (1,3) है ✅। Step 3: अतः R संक्रमणशील संबंध है।
🔟 कार्टेशियन गुणनफल (Cartesian Product) दो समुच्चयों A और B का कार्टेशियन गुणनफल A × B है, जिसमें सभी संभव युग्म (a, b) होते हैं, जहाँ a ∈ A और b ∈ B। 👉 उदाहरण 10: A = {1,2} और B = {3,4} है। A × B ज्ञात कीजिए। Step 1: A × B = {(1,3), (1,4), (2,3), (2,4)} Step 2: यह सभी युग्म हैं जो A और B के तत्वों से बनते हैं। Step 3: अतः A × B = {(1,3), (1,4), (2,3), (2,4)} है।
1️⃣1️⃣ समतुल्यता संबंध (Equivalence Relation) यदि एक संबंध reflexive, symmetric और transitive हो, तो उसे समतुल्यता संबंध कहते हैं। 👉 उदाहरण 11: A = {1,2,3} और R = {(1,1), (2,2), (3,3), (1,2), (2,1)} है। जाँचिए कि R समतुल्यता संबंध है या नहीं। Step 1: Reflexive: (1,1), (2,2), (3,3) हैं ✅। Step 2: Symmetric: (1,2) और (2,1) हैं ✅। Step 3: Transitive: (1,2) और (2,1) होने पर (1,1) होना चाहिए, जो है ✅। Step 4: सभी गुण (Reflexive, Symmetric, Transitive) पूर्ण होने पर, R समतुल्यता संबंध है।

क्रमांक 🔢 व Formula 📖 + Explanation ✍️ + Example 🎯

1️⃣ संबंध (Relation) की परिभाषा

यदि A और B दो गैर-रिक्त समुच्चय हैं, तो A × B = {(a,b) | a ∈ A और b ∈ B} कहलाता है।

👉 उदाहरण 1: यदि A = {1,2} और B = {3,4} तो A × B ज्ञात कीजिए।

Step 1: A के प्रत्येक तत्त्व को B के प्रत्येक तत्त्व से जोड़ना।
Step 2: युग्म मिलेंगे: (1,3), (1,4), (2,3), (2,4)
Step 3: अतः A × B = {(1,3), (1,4), (2,3), (2,4)}

2️⃣ परावर्ती संबंध (Reflexive Relation)

यदि प्रत्येक a ∈ A के लिए (a,a) ∈ R हो, तो संबंध परावर्ती होता है।

👉 उदाहरण 2: A = {1,2} और R = {(1,1), (2,2)} है। जाँचिए कि R परावर्ती है या नहीं।

Step 1: 1 के लिए (1,1) है ✅ और 2 के लिए (2,2) है ✅।
Step 2: सभी तत्त्व स्वयं से जुड़े हैं।
Step 3: अतः R परावर्ती संबंध है।

3️⃣ प्रत्यावर्ती संबंध (Symmetric Relation)

यदि (a,b) ∈ R ⇒ (b,a) ∈ R, तो संबंध प्रत्यावर्ती होता है।

👉 उदाहरण 3: A = {1,2} और R = {(1,2), (2,1)} है। जाँचिए कि R प्रत्यावर्ती है या नहीं।

Step 1: (1,2) है और उसके साथ (2,1) भी है ✅।
Step 2: दोनों ओर समानता है।
Step 3: अतः R प्रत्यावर्ती संबंध है।

4️⃣ पारगम्य संबंध (Transitive Relation)

यदि (a,b) ∈ R और (b,c) ∈ R हो ⇒ (a,c) ∈ R, तो संबंध पारगम्य होता है।

👉 उदाहरण 4: A = {1,2,3} और R = {(1,2), (2,3), (1,3)} है। जाँचिए कि R पारगम्य है या नहीं।

Step 1: (1,2) और (2,3) है ⇒ तो (1,3) होना चाहिए।
Step 2: (1,3) है ✅।
Step 3: अतः R पारगम्य संबंध है।

5️⃣ सार्वत्रिक संबंध (Universal Relation)

यदि R = A × A हो, अर्थात् प्रत्येक संभव युग्म (a,b) ∈ R हो, तो संबंध सार्वत्रिक होता है।

👉 उदाहरण 5: A = {1,2} के लिए R = {(1,1), (1,2), (2,1), (2,2)} है। जाँचिए कि R सार्वत्रिक है या नहीं।

Step 1: सभी संभव युग्म (1,1), (1,2), (2,1), (2,2) मौजूद हैं।
Step 2: कोई भी युग्म छूटा नहीं है।
Step 3: अतः R सार्वत्रिक संबंध है।

6️⃣ रिक्त संबंध (Empty Relation)

यदि R = ∅ हो (कोई भी युग्म नहीं हो), तो संबंध रिक्त कहलाता है।

👉 उदाहरण 6: A = {1,2,3} और R = ∅ है।

Step 1: R में कोई भी युग्म नहीं है।
Step 2: कोई भी तत्त्व आपस में संबंधित नहीं है।
Step 3: अतः यह रिक्त संबंध है।

7️⃣ एक-एक संबंध (One-One Relation)

अगर प्रत्येक तत्त्व A का अलग-अलग तत्त्वों से B में मेल हो, तो उसे एक-एक संबंध कहते हैं।

👉 उदाहरण 7: A = {1,2,3}, B = {4,5,6} और R = {(1,4), (2,5), (3,6)} है।

Step 1: 1 → 4, 2 → 5, 3 → 6।
Step 2: कोई दो तत्त्व एक ही तत्त्व से नहीं जुड़े।
Step 3: अतः यह एक-एक संबंध है।

8️⃣ कार्यात्मक संबंध (Functional Relation)

अगर A का प्रत्येक तत्त्व B के केवल एक तत्त्व से जुड़ा हो, तो उसे कार्यात्मक संबंध कहते हैं।

👉 उदाहरण 8: A = {a,b} और B = {1,2,3}, R = {(a,2), (b,3)} है।

Step 1: a केवल 2 से और b केवल 3 से जुड़ा है।
Step 2: हर तत्त्व का एक ही output है।
Step 3: अतः R एक कार्यात्मक संबंध है।

9️⃣ संक्रमणशील संबंध (Transitive Relation)

यदि (a,b) ∈ R और (b,c) ∈ R हो, तो (a,c) ∈ R भी होना चाहिए, तब इसे संक्रमणशील संबंध कहते हैं।

👉 उदाहरण 9: A = {1,2,3} और R = {(1,2), (2,3), (1,3)} है। जाँचिए कि R संक्रमणशील है या नहीं।

Step 1: (1,2) और (2,3) है ⇒ तो (1,3) होना चाहिए।
Step 2: (1,3) है ✅।
Step 3: अतः R संक्रमणशील संबंध है।

🔟 कार्टेशियन गुणनफल (Cartesian Product)

दो समुच्चयों A और B का कार्टेशियन गुणनफल A × B है, जिसमें सभी संभव युग्म (a, b) होते हैं, जहाँ a ∈ A और b ∈ B।

👉 उदाहरण 10: A = {1,2} और B = {3,4} है। A × B ज्ञात कीजिए।

Step 1: A × B = {(1,3), (1,4), (2,3), (2,4)}
Step 2: यह सभी युग्म हैं जो A और B के तत्वों से बनते हैं।
Step 3: अतः A × B = {(1,3), (1,4), (2,3), (2,4)} है।

1️⃣1️⃣ समतुल्यता संबंध (Equivalence Relation)

यदि एक संबंध reflexive, symmetric और transitive हो, तो उसे समतुल्यता संबंध कहते हैं।

👉 उदाहरण 11: A = {1,2,3} और R = {(1,1), (2,2), (3,3), (1,2), (2,1)} है। जाँचिए कि R समतुल्यता संबंध है या नहीं।

Step 1: Reflexive: (1,1), (2,2), (3,3) हैं ✅।
Step 2: Symmetric: (1,2) और (2,1) हैं ✅।
Step 3: Transitive: (1,2) और (2,1) होने पर (1,1) होना चाहिए, जो है ✅।
Step 4: सभी गुण (Reflexive, Symmetric, Transitive) पूर्ण होने पर, R समतुल्यता संबंध है।

🔹 फलन (Function) के Formulas 🔹

क्रमांक 🔢 व Formula 📖 + Explanation ✍️ + Example 🎯
1️⃣ फलन (Function) की परिभाषा एक संबंध f: A → B फलन है यदि A का प्रत्येक तत्त्व B के केवल एक तत्त्व से जुड़ा हो। 👉 उदाहरण 1: यदि A = {1,2} और B = {3,4}, तो: A × B = {(1,3), (1,4), (2,3), (2,4)} है, लेकिन यह फलन नहीं है क्योंकि 1 का 2 से जुड़ा है।
2️⃣ एक-एक फलन (One-to-One Function) यदि फलन f: A → B में A का प्रत्येक तत्त्व B के अलग-अलग तत्त्व से जुड़ा हो, तो इसे एक-एक फलन कहते हैं। 👉 उदाहरण 2: यदि A = {1, 2} और B = {3, 4}, तो: f(1) = 3, f(2) = 4 यह एक-एक फलन है क्योंकि प्रत्येक A का तत्त्व B के अलग-अलग तत्त्व से जुड़ा है।
3️⃣ onto फलन (Onto Function) यदि B के प्रत्येक तत्त्व से कम से कम एक तत्त्व A में जुड़ा हो, तो इसे onto फलन कहते हैं। 👉 उदाहरण 3: यदि A = {1,2} और B = {3,4}, तो: f(1) = 3, f(2) = 4 यह onto फलन है क्योंकि B का हर तत्त्व A के किसी तत्त्व से जुड़ा है।
4️⃣ बायिजेक्टिव फलन (Bijective Function) फलन f: A → B को बायिजेक्टिव फलन कहा जाता है यदि वह एक-एक (One-to-One) और onto दोनों हो। 👉 उदाहरण 4: यदि A = {1,2} और B = {3,4}, तो: f(1) = 3, f(2) = 4 यह बायिजेक्टिव फलन है क्योंकि यह एक-एक और onto दोनों है।
5️⃣ फलन का रेंज (Range of a Function) फलन के उस भाग को रेंज कहते हैं, जो B के तत्वों के समूह में से प्राप्त होता है। 👉 उदाहरण 5: यदि A = {1, 2} और B = {3, 4, 5}, और f(1) = 3, f(2) = 4 है, तो: रेंज = {3, 4}

क्रमांक 🔢 व Formula 📖 + Explanation ✍️ + Example 🎯

1️⃣ फलन (Function) की परिभाषा

एक संबंध f: A → B फलन है यदि A का प्रत्येक तत्त्व B के केवल एक तत्त्व से जुड़ा हो।

👉 उदाहरण 1: यदि A = {1,2} और B = {3,4}, तो:

A × B = {(1,3), (1,4), (2,3), (2,4)} है, लेकिन यह फलन नहीं है क्योंकि 1 का 2 से जुड़ा है।

2️⃣ एक-एक फलन (One-to-One Function)

यदि फलन f: A → B में A का प्रत्येक तत्त्व B के अलग-अलग तत्त्व से जुड़ा हो, तो इसे एक-एक फलन कहते हैं।

👉 उदाहरण 2: यदि A = {1, 2} और B = {3, 4}, तो:

f(1) = 3, f(2) = 4
यह एक-एक फलन है क्योंकि प्रत्येक A का तत्त्व B के अलग-अलग तत्त्व से जुड़ा है।

3️⃣ onto फलन (Onto Function)

यदि B के प्रत्येक तत्त्व से कम से कम एक तत्त्व A में जुड़ा हो, तो इसे onto फलन कहते हैं।

👉 उदाहरण 3: यदि A = {1,2} और B = {3,4}, तो:

f(1) = 3, f(2) = 4
यह onto फलन है क्योंकि B का हर तत्त्व A के किसी तत्त्व से जुड़ा है।

4️⃣ बायिजेक्टिव फलन (Bijective Function)

फलन f: A → B को बायिजेक्टिव फलन कहा जाता है यदि वह एक-एक (One-to-One) और onto दोनों हो।

👉 उदाहरण 4: यदि A = {1,2} और B = {3,4}, तो:

f(1) = 3, f(2) = 4
यह बायिजेक्टिव फलन है क्योंकि यह एक-एक और onto दोनों है।

5️⃣ फलन का रेंज (Range of a Function)

फलन के उस भाग को रेंज कहते हैं, जो B के तत्वों के समूह में से प्राप्त होता है।

👉 उदाहरण 5: यदि A = {1, 2} और B = {3, 4, 5}, और f(1) = 3, f(2) = 4 है, तो:

रेंज = {3, 4}

Trigonometry

Radian and Degree Measures of Angles:

1 rad	180°π ≈ 57°17'45"
1°	π180rad ≈ 0.017453
1'	π180.60rad ≈ 0.000291 rad
1"	π180.3600rad ≈ 0.000005 rad

Trigonometric Ratio

Opposite Side = लम्ब

Hypotenuse = कर्ण

Adjacent Side = आधार

(कर्ण)²	(लम्ब)² + (आधार)²
(लम्ब)²	(कर्ण)² - (आधार)²
(आधार)²	(कर्ण)² - (लम्ब)²
sin θ	लम्बकर्ण
cos θ	आधारकर्ण
tan θ	लम्बआधार
cosec θ	कर्णलम्ब , 1Sin
sec θ	कर्णआधार , 1cos
cot θ	आधारलम्ब , 1tan

Reciprocal Identities:

cosec θ	1sin θ
sec θ	1cos θ
cot θ	1tan θ

Quotient Identities:

tan θ	sin θcos θ
cot θ	cos θsin θ

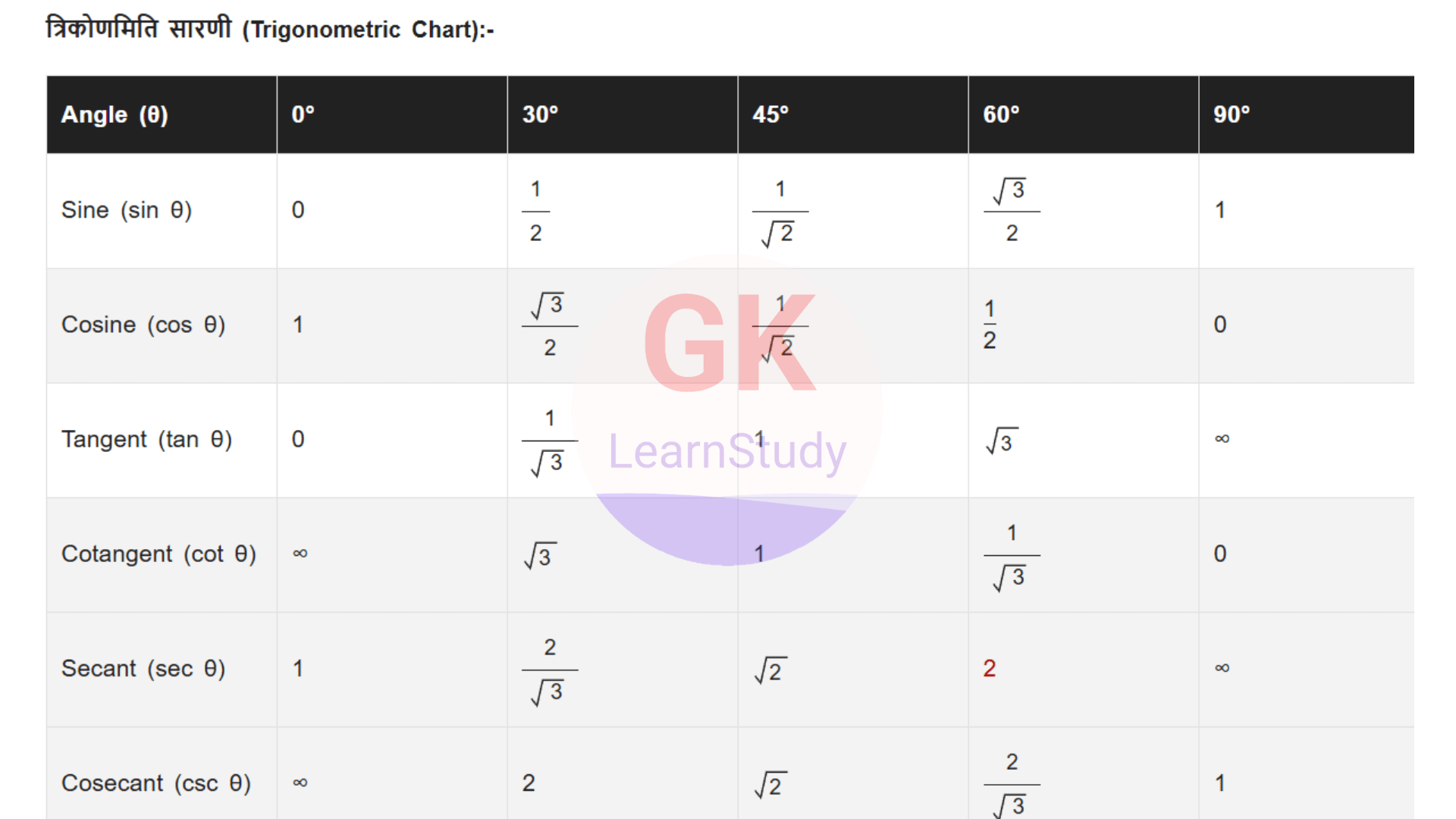
त्रिकोणमिति सारणी (Trigonometric Chart):-

Angle (θ)	0°	30°	45°	60°	90°
Sine (sin θ)	0	12	12	32	1
Cosine (cos θ)	1	32	12	12	0
Tangent (tan θ)	0	13	1	3	∞
Cotangent (cot θ)	∞	3	1	13	0
Secant (sec θ)	1	23	2	2	∞
Cosecant (csc θ)	∞	2	2	23	1

Pythagorean Identities:

sin² θ + cos² θ	1
sec² θ - tan² θ	1
cosec² θ - cot² θ	1

Even-Odd Identities:

sin(-θ)	-sin(θ)
cos(-θ)	cos(θ)
tan(-θ)	-tan(θ)
csc(-θ)	-csc(θ)
sec(-θ)	sec(θ)
cot(-θ)	-cot(θ)

Co - Ratio

Trigonometric Identities

Angle	sin	cos	tan	cot	sec	csc
90 - θ	cos(θ)	sin(θ)	cot(θ)	tan(θ)	csc(θ)	sec(θ)
90 + θ	cos(θ)	-sin(θ)	-cot(θ)	-tan(θ)	-csc(θ)	sec(θ)
180 - θ	sin(θ)	-cos(θ)	-tan(θ)	-cot(θ)	-sec(θ)	csc(θ)
180 + θ	-sin(θ)	-cos(θ)	tan(θ)	cot(θ)	-sec(θ)	-csc(θ)

Relations between Trigonometric Functions

Addition and Subtraction Formulas

sin(x + y)	sin x cos y + sin y cos x
sin(x - y)	sin x cos y - sin y cos x
cos(x + y)	- cos x cos y - sin x sin y
cos(x - y)	- cos x cos y + sin x sin y
tan (x + y)	tan x + tan y1 - tan x . tan y
tan (x - y)	tan x - tan y1 + tan x . tan y
cot (x + y)	1 - tan x . tan ytan x + tan y
cot (x - y)	1 + tan x . tan ytan x - tan y

Double Angle Formulas

sin 2θ	2sinθcosθ
cos 2θ	cos²θ-sin²θ Or 1-2sin²θ Or 2 cos²θ-1
tan 2θ	2 tanθ1-tan²θ or 2cotθ - tanθ
cot 2θ	cot²θ - 12 cotθ or cotθ - tanθ2

Multiple Angle Formulas

sin 3θ	3 sinθ−4 sin³θ Or 3 cos²θ.sinθ - sin³θ
sin 4θ	4 sinθ.cosθ - 8 sin³θ.cosθ
sin 5θ	5 sinθ-20 sin³θ + 16 sin⁵θ
cos 3θ	4 cos³θ − 3 cosθ = cos³θ . sin²θ
cos 4θ	8 cos⁴θ − 8 cos²θ + 1
cos 5θ	16 cos⁵θ − 20 cos³θ + 5 cosθ
tan 3θ	3 tan θ - tan³θ1 - 3 tan²θ
tan 4θ	4 tan θ - 4 tan³θ1 - 6 tan²θ + tan⁴θ
tan 5θ	tan⁵θ - 10 tan³θ + 5 tanθ1 - 10 tan²θ + 5 tan⁴θ
cot 3θ	cot³θ - 3 cot θ3 cot²θ - 1
cot 4θ	1 - 6 tan²θ + tan⁴θ4 tan θ - 4 tan³θ
cot 5θ	1 - 10 tan²θ + 5 tan⁴θtan⁵θ - 10 tan³θ + 5 tan θ

Periodic Identities

Identity	Formula
Sine (साइन)	sin(θ + 2π) = sin θ sin(θ + 360°) = sin θ
Cosine (कोसाइन)	cos(θ + 2π) = cos θ cos(θ + 360°) = cos θ
Tangent (टैनजेंट)	tan(θ + π) = tan θ tan(θ + 180°) = tan θ
Cotangent (कोटेंजेंट)	cot(θ + π) = cot θ cot(θ + 180°) = cot θ
Secant (सेकेंट)	sec(θ + 2π) = sec θ sec(θ + 360°) = sec θ
Cosecant (कोसेकेंट)	csc(θ + 2π) = csc θ csc(θ + 360°) = csc θ

Half Angle Formulas

Function	Half-Angle Formula
sin(θ/2)	± ((1 - cos(θ)) / 2)
cos(θ/2)	± ((1 + cos(θ)) / 2)
tan(θ/2)	± ((1 - cos(θ)) / (1 + cos(θ)))
tan(θ/2)	sin(θ) / (1 + cos(θ))
tan(θ/2)	(1 - cos(θ)) / sin(θ)
sec(θ/2)	± ((2) / (1 + cos(θ)))
csc(θ/2)	± ((2) / (1 - cos(θ)))
cot(θ/2)	± ((1 + cos(θ)) / (1 - cos(θ)))
sec(θ/2)	(1 + cos(θ)) / cos(θ)
csc(θ/2)	(1 - cos(θ)) / sin(θ)
cot(θ/2)	(1 + cos(θ)) / sin(θ)
sec(θ/2)	1 / cos(θ/2)
csc(θ/2)	1 / sin(θ/2)
cot(θ/2)	1 / tan(θ/2)
sin α	2 tan(α2) 1 + tan²(α2)

Product to Sum Formulas:

Identity	Formula
Sine and Cosine	sin A cos B = ½ [sin (A + B) + sin (A - B)] cos A sin B = ½ [sin (A + B) - sin (A - B)] cos A cos B = ½ [cos (A + B) + cos (A - B)] sin A sin B = ½ [cos (A - B) - cos (A + B)]

Identity

Formula

Sine and Cosine

sin A cos B = ½ [sin (A + B) + sin (A - B)]

cos A sin B = ½ [sin (A + B) - sin (A - B)]

cos A cos B = ½ [cos (A + B) + cos (A - B)]

sin A sin B = ½ [cos (A - B) - cos (A + B)]

Sum to Product Formulas

Identity	Formula
Sine and Cosine	sin A + sin B = 2 sin (½ (A + B)) cos (½ (A - B)) sin A - sin B = 2 cos (½ (A + B)) sin (½ (A - B)) cos A + cos B = 2 cos (½ (A + B)) cos (½ (A - B)) cos A - cos B = -2 sin (½ (A + B)) sin (½ (A - B))

Identity

Formula

Sine and Cosine

sin A + sin B = 2 sin (½ (A + B)) cos (½ (A - B))

sin A - sin B = 2 cos (½ (A + B)) sin (½ (A - B))

cos A + cos B = 2 cos (½ (A + B)) cos (½ (A - B))

cos A - cos B = -2 sin (½ (A + B)) sin (½ (A - B))

Law of Sines (साइन का नियम)

Formula	Explanation
a / sin A = b / sin B = c / sin C	This formula states that the ratio of each side of a triangle to the sine of its opposite angle is constant.

Law of Cosines (कोसाइन का नियम)

Formula	Explanation
c² = a² + b² - 2ab cos C	This formula relates the lengths of the sides of a triangle to the cosine of one of its angles.
a² = b² + c² - 2bc cos A	Relates the length of side a to the cosine of angle A.
b² = a² + c² - 2ac cos B	Relates the length of side b to the cosine of angle B.

Law of Tangents (टैनजेंट का नियम)

Formula	Explanation
tan [(A ± B) / 2] = (tan A ± tan B) / (1 ∓ tan A tan B)	This formula relates the tangent of half-angle sums or differences to the tangents of the angles themselves.

Area of a Triangle Using Trigonometry (त्रिकोण का क्षेत्रफल त्रिकोणमिति का उपयोग करके)

Formula	Explanation
Area = ½ ab sin C	The area of a triangle can be calculated using the lengths of two sides and the sine of the included angle.

Chebyshev Polynomials (चेबिशेव बहुपद)

Polynomial	Formula
First Kind (प्रथम प्रकार)	Tₙ(x) = cos(n cos⁻¹(x))
Second Kind (द्वितीय प्रकार)	Uₙ(x) = sin((n+1) cos⁻¹(x)) / sin(cos⁻¹(x))

Exponential Form of Trigonometric Functions (त्रिकोणमितीय संख्याओं के घातांक रूप)

Function	Formula
Euler's Formulas (यूलर के फॉर्मूला)	e^(iθ) = cos(θ) + i sin(θ) e^(-iθ) = cos(θ) - i sin(θ)
sin(θ) and cos(θ)	sin(θ) = (e^(iθ) - e^(-iθ)) / 2i cos(θ) = (e^(iθ) + e^(-iθ)) / 2

Function

Formula

Euler's Formulas (यूलर के फॉर्मूला)

e^(iθ) = cos(θ) + i sin(θ)

e^(-iθ) = cos(θ) - i sin(θ)

sin(θ) and cos(θ)

sin(θ) = (e^(iθ) - e^(-iθ)) / 2i

cos(θ) = (e^(iθ) + e^(-iθ)) / 2

Sum and Difference Identities for Inverse Trigonometric Functions (प्रतिलोम त्रिकोणमितीय संख्याओं के योग और अंतर संख्याएँ)

Identity	Formula
Sum Formulas (योग फॉर्मूला)	sin⁻¹(x) + sin⁻¹(y) = sin⁻¹(x 1-y² + y 1-x²) cos⁻¹(x) + cos⁻¹(y) = cos⁻¹(xy - 1-x² 1-y²) tan⁻¹(x) + tan⁻¹(y) = tan⁻¹((x + y) / (1 - xy))
Difference Formulas (अंतर फॉर्मूला)	sin⁻¹(x) - sin⁻¹(y) = sin⁻¹(x 1-y² - y 1-x²) cos⁻¹(x) - cos⁻¹(y) = cos⁻¹(xy + 1-x² 1-y²) tan⁻¹(x) - tan⁻¹(y) = tan⁻¹((x - y) / (1 + xy))

Identity

Formula

Sum Formulas (योग फॉर्मूला)

sin⁻¹(x) + sin⁻¹(y) = sin⁻¹(x 1-y² + y 1-x²)

cos⁻¹(x) + cos⁻¹(y) = cos⁻¹(xy - 1-x² 1-y²)

tan⁻¹(x) + tan⁻¹(y) = tan⁻¹((x + y) / (1 - xy))

Difference Formulas (अंतर फॉर्मूला)

sin⁻¹(x) - sin⁻¹(y) = sin⁻¹(x 1-y² - y 1-x²)

cos⁻¹(x) - cos⁻¹(y) = cos⁻¹(xy + 1-x² 1-y²)

tan⁻¹(x) - tan⁻¹(y) = tan⁻¹((x - y) / (1 + xy))

Transformations Using Trigonometric Identities (त्रिकोणमितीय संख्याओं का उपयोग करके रूपांतरण)

Transformation	Formula
sin(θ + 90°)	cos(θ)
cos(θ + 90°)	-sin(θ)
tan(θ + 90°)	-cot(θ)
cot(θ + 90°)	-tan(θ)
sec(θ + 90°)	-csc(θ)
csc(θ + 90°)	sec(θ)

Inverse Trigonometric Identities (प्रतिलोम त्रिकोणमितीय संख्याएँ)

Function	Formula
Inverse Sine (आर्कसाइन)	sin^-1(x) = θ, where sin θ = x
Inverse Cosine (आर्ककोसाइन)	cos^-1(x) = θ, where cos θ = x
Inverse Tangent (आर्कटैनजेंट)	tan^-1(x) = θ, where tan θ = x
Inverse Cotangent (आर्ककोटेंजेंट)	cot^-1(x) = θ, where cot θ = x
Inverse Secant (आर्कसेकेंट)	sec^-1(x) = θ, where sec θ = x
Inverse Cosecant (आर्ककोसेकेंट)	csc^-1(x) = θ, where csc θ = x

Principal Values of Inverse Trigonometric Functions (प्रतिलोम त्रिकोणमितीय संख्याओं के मुख्य मान)

Function	Principal Value
sin⁻¹(x)	[-π/2, π/2]
cos⁻¹(x)	[0, π]
tan⁻¹(x)	[-π/2, π/2]
cot⁻¹(x)	[0, π]
sec⁻¹(x)	[0, π] except π/2
csc⁻¹(x)	[-π/2, π/2] except 0

General Solutions of Trigonometric Equations (त्रिकोणमितीय समीकरणों के सामान्य समाधान)

Equation	General Solution
sin(θ) = 0	θ = nπ, where n ∈ ℤ
cos(θ) = 0	θ = (2n+1)π/2, where n ∈ ℤ
tan(θ) = 0	θ = nπ, where n ∈ ℤ
sin(θ) = a	θ = nπ + (-1)ⁿ arcsin(a), where n ∈ ℤ
cos(θ) = a	θ = 2nπ ± arccos(a), where n ∈ ℤ
tan(θ) = a	θ = nπ + arctan(a), where n ∈ ℤ
cot(θ) = a	θ = nπ + arccot(a), where n ∈ ℤ
sec(θ) = a	θ = 2nπ ± arcsec(a), where n ∈ ℤ
csc(θ) = a	θ = nπ + (-1)ⁿ arccsc(a), where n ∈ ℤ

🔹 सम्मिश्र संख्याएँ (Complex Numbers) के Formulas 🔹

क्रमांक 🔢 व Formula 📖 + Explanation ✍️ + Example 🎯
1️⃣ सम्मिश्र संख्या (Complex Number) की परिभाषा सम्मिश्र संख्या को z = a + bi के रूप में व्यक्त किया जाता है, जहाँ a और b वास्तविक संख्याएँ हैं, और i = (-1) है। 👉 उदाहरण 1: यदि z = 3 + 4i, तो: a = 3, b = 4 यह एक सम्मिश्र संख्या है।
2️⃣ सम्मिश्र संख्याओं का जोड़ (Addition of Complex Numbers) यदि z₁ = a + bi और z₂ = c + di, तो: z₁ + z₂ = (a + c) + (b + d)i 👉 उदाहरण 2: यदि z₁ = 3 + 2i और z₂ = 1 + 4i, तो: z₁ + z₂ = (3+1) + (2+4)i = 4 + 6i
3️⃣ सम्मिश्र संख्याओं का गुणन (Multiplication of Complex Numbers) यदि z₁ = a + bi और z₂ = c + di, तो: z₁ × z₂ = (ac - bd) + (ad + bc)i 👉 उदाहरण 3: यदि z₁ = 2 + 3i और z₂ = 1 + 2i, तो: z₁ × z₂ = (2×1 - 3×2) + (2×2 + 3×1)i = -4 + 7i
4️⃣ सम्मिश्र संख्याओं का अभ्युत्थान (Conjugate of a Complex Number) सम्मिश्र संख्या z = a + bi का अभ्युत्थान z* = a - bi होता है। 👉 उदाहरण 4: यदि z = 3 + 4i, तो: z* = 3 - 4i
5️⃣ सम्मिश्र संख्या का विभाजन (Division of Complex Numbers) यदि z₁ = a + bi और z₂ = c + di, तो: z₁ ÷ z₂ = (a + bi) ÷ (c + di) = [(a + bi)(c - di)] ÷ (c² + d²) 👉 उदाहरण 5: यदि z₁ = 2 + 3i और z₂ = 1 + 2i, तो: z₁ ÷ z₂ = [(2+3i)(1-2i)] ÷ (1² + 2²) = (2 - 4i + 3i - 6) ÷ 5 = (-4 - i) ÷ 5 = -4/5 - i/5
6️⃣ सम्मिश्र संख्या का मान (Modulus of a Complex Number) सम्मिश्र संख्या z = a + bi का मान \|z\| = (a² + b²) होता है। 👉 उदाहरण 6: यदि z = 3 + 4i, तो: \|z\| = (3² + 4²) = (9 + 16) = 25 = 5
7️⃣ सम्मिश्र संख्या का आर्कटंगेंट (Argument of a Complex Number) सम्मिश्र संख्या z = a + bi का आर्कटंगेंट (argument) θ = tan⁻¹(b/a) होता है, जहाँ a और b वास्तविक संख्याएँ हैं। 👉 उदाहरण 7: यदि z = 3 + 4i, तो: θ = tan⁻¹(4/3) ≈ 0.93
8️⃣ सम्मिश्र संख्या का polar रूप (Polar Form of a Complex Number) सम्मिश्र संख्या को Polar रूप में z = r (cos θ + i sin θ) के रूप में लिखा जाता है, जहाँ r = \|z\| और θ = argument(z) होता है। 👉 उदाहरण 8: यदि z = 3 + 4i, तो: r = (3² + 4²) = 5 θ = tan⁻¹(4/3) ≈ 0.93 Polar रूप: z = 5 (cos 0.93 + i sin 0.93)
9️⃣ सम्मिश्र संख्या का Exponential रूप (Exponential Form of a Complex Number) सम्मिश्र संख्या को Exponential रूप में z = r e^(iθ) के रूप में लिखा जाता है, जहाँ r = \|z\| और θ = argument(z) होता है। 👉 उदाहरण 9: यदि z = 3 + 4i, तो: r = 5, θ = 0.93 Exponential रूप: z = 5 e^(i 0.93)
🔟 सम्मिश्र संख्या का रियल और इमेजिनरी भाग (Real and Imaginary Parts) सम्मिश्र संख्या z = a + bi में: रियल भाग = a इमेजिनरी भाग = b 👉 उदाहरण 10: यदि z = 5 + 6i, तो: रियल भाग = 5 इमेजिनरी भाग = 6
1️⃣1️⃣ सम्मिश्र संख्या का पोलर रूप से कार्टेशियन रूप में परिवर्तन (Polar to Cartesian Conversion) यदि एक सम्मिश्र संख्या z = r (cos θ + i sin θ) है, तो इसका कार्टेशियन रूप (a + bi) इस प्रकार होगा: a = r cos θ b = r sin θ 👉 उदाहरण 1: यदि z = 5 (cos 0.93 + i sin 0.93), तो: a = 5 cos 0.93 ≈ 3 b = 5 sin 0.93 ≈ 4 तो z = 3 + 4i
1️⃣2️⃣ सम्मिश्र संख्या का कार्टेशियन रूप से पोलर रूप में परिवर्तन (Cartesian to Polar Conversion) यदि एक सम्मिश्र संख्या z = a + bi है, तो इसका पोलर रूप इस प्रकार होगा: r = (a² + b²) θ = tan⁻¹(b/a) 👉 उदाहरण 2: यदि z = 3 + 4i, तो: r = (3² + 4²) = 5 θ = tan⁻¹(4/3) ≈ 0.93 पोलर रूप: z = 5 (cos 0.93 + i sin 0.93)
1️⃣3️⃣ सम्मिश्र संख्या का De Moivre's Theorem De Moivre's Theorem के अनुसार, यदि z = r (cos θ + i sin θ) है, तो: zⁿ = rⁿ [cos(nθ) + i sin(nθ)] 👉 उदाहरण 3: यदि z = 2 (cos 30° + i sin 30°), और n = 3, तो: z³ = 2³ [cos(90°) + i sin(90°)] = 8i
1️⃣4️⃣ सम्मिश्र संख्याओं का जड़ (Roots of Complex Numbers) यदि z = r (cos θ + i sin θ) हो, तो z की n जड़ें निम्न प्रकार होंगी: z_k = r^1/n [cos((θ + 2πk) / n) + i sin((θ + 2πk) / n)] जहाँ k = 0, 1, 2, ..., n − 1 👉 उदाहरण 4: यदि z = 1 (cos 60° + i sin 60°), और n = 2, तो: z₀ = 1^1/2 [cos(60° / 2) + i sin(60° / 2)] = cos 30° + i sin 30° z₁ = 1^1/2 [cos((60° + 360°) / 2) + i sin((60° + 360°) / 2)] = cos 150° + i sin 150°
1️⃣5️⃣ सम्मिश्र संख्याओं का ट्रिगोनोमेट्रिक रूप (Trigonometric Form) सम्बन्धित ट्रिगोनोमेट्रिक रूप में: z = r [cos(θ) + i sin(θ)] 👉 उदाहरण 5: यदि z = 3 + 4i, तो: r = (3² + 4²) = 5 θ = tan⁻¹(4/3) ≈ 0.93 तो ट्रिगोनोमेट्रिक रूप: z = 5 [cos(0.93) + i sin(0.93)]
1️⃣6️⃣ सम्मिश्र संख्याओं का क्यूब (Cube of a Complex Number) यदि z = a + bi है, तो z का क्यूब निम्नलिखित होगा: z³ = (a + bi)³ = a³ + 3a²bi + 3ab²i² + b³i³ यहाँ i² = -1 और i³ = -i होता है। 👉 उदाहरण 6: यदि z = 1 + 2i, तो: z³ = (1 + 2i)³ = 1³ + 3(1²)(2i) + 3(1)(2²)(-1) + (2³)(-i) z³ = 1 + 6i - 12 - 8i = -11 - 2i
1️⃣7️⃣ सम्मिश्र संख्याओं का नकारात्मक घनमूल (Negative Cube Root) किसी सम्मिश्र संख्या का नकारात्मक घनमूल निकालने के लिए: (-z)^1/3 = r^1/3 [cos((θ + 180°) / 3) + i sin((θ + 180°) / 3)] 👉 उदाहरण 7: यदि z = -8, तो: r = 8, θ = 180° (-8)^1/3 = 2 [cos(60°) + i sin(60°)] (-8)^1/3 = 2(1/2 + i3/2) = 1 + i3

क्रमांक 🔢 व Formula 📖 + Explanation ✍️ + Example 🎯

1️⃣ सम्मिश्र संख्या (Complex Number) की परिभाषा

सम्मिश्र संख्या को z = a + bi के रूप में व्यक्त किया जाता है, जहाँ a और b वास्तविक संख्याएँ हैं, और i = (-1) है।

👉 उदाहरण 1: यदि z = 3 + 4i, तो:

a = 3, b = 4
यह एक सम्मिश्र संख्या है।

2️⃣ सम्मिश्र संख्याओं का जोड़ (Addition of Complex Numbers)

यदि z₁ = a + bi और z₂ = c + di, तो:

z₁ + z₂ = (a + c) + (b + d)i

👉 उदाहरण 2: यदि z₁ = 3 + 2i और z₂ = 1 + 4i, तो:

z₁ + z₂ = (3+1) + (2+4)i = 4 + 6i

3️⃣ सम्मिश्र संख्याओं का गुणन (Multiplication of Complex Numbers)

यदि z₁ = a + bi और z₂ = c + di, तो:

z₁ × z₂ = (ac - bd) + (ad + bc)i

👉 उदाहरण 3: यदि z₁ = 2 + 3i और z₂ = 1 + 2i, तो:

z₁ × z₂ = (2×1 - 3×2) + (2×2 + 3×1)i = -4 + 7i

4️⃣ सम्मिश्र संख्याओं का अभ्युत्थान (Conjugate of a Complex Number)

सम्मिश्र संख्या z = a + bi का अभ्युत्थान z* = a - bi होता है।

👉 उदाहरण 4: यदि z = 3 + 4i, तो:

z* = 3 - 4i

5️⃣ सम्मिश्र संख्या का विभाजन (Division of Complex Numbers)

यदि z₁ = a + bi और z₂ = c + di, तो:

z₁ ÷ z₂ = (a + bi) ÷ (c + di) = [(a + bi)(c - di)] ÷ (c² + d²)

👉 उदाहरण 5: यदि z₁ = 2 + 3i और z₂ = 1 + 2i, तो:

z₁ ÷ z₂ = [(2+3i)(1-2i)] ÷ (1² + 2²) = (2 - 4i + 3i - 6) ÷ 5 = (-4 - i) ÷ 5 = -4/5 - i/5

6️⃣ सम्मिश्र संख्या का मान (Modulus of a Complex Number)

सम्मिश्र संख्या z = a + bi का मान |z| = (a² + b²) होता है।

👉 उदाहरण 6: यदि z = 3 + 4i, तो:

|z| = (3² + 4²) = (9 + 16) = 25 = 5

7️⃣ सम्मिश्र संख्या का आर्कटंगेंट (Argument of a Complex Number)

सम्मिश्र संख्या z = a + bi का आर्कटंगेंट (argument) θ = tan⁻¹(b/a) होता है, जहाँ a और b वास्तविक संख्याएँ हैं।

👉 उदाहरण 7: यदि z = 3 + 4i, तो:

θ = tan⁻¹(4/3) ≈ 0.93

8️⃣ सम्मिश्र संख्या का polar रूप (Polar Form of a Complex Number)

सम्मिश्र संख्या को Polar रूप में z = r (cos θ + i sin θ) के रूप में लिखा जाता है, जहाँ r = |z| और θ = argument(z) होता है।

👉 उदाहरण 8: यदि z = 3 + 4i, तो:

r = (3² + 4²) = 5
θ = tan⁻¹(4/3) ≈ 0.93
Polar रूप: z = 5 (cos 0.93 + i sin 0.93)

9️⃣ सम्मिश्र संख्या का Exponential रूप (Exponential Form of a Complex Number)

सम्मिश्र संख्या को Exponential रूप में z = r e^(iθ) के रूप में लिखा जाता है, जहाँ r = |z| और θ = argument(z) होता है।

👉 उदाहरण 9: यदि z = 3 + 4i, तो:

r = 5, θ = 0.93
Exponential रूप: z = 5 e^(i 0.93)

🔟 सम्मिश्र संख्या का रियल और इमेजिनरी भाग (Real and Imaginary Parts)

सम्मिश्र संख्या z = a + bi में:

रियल भाग = a
इमेजिनरी भाग = b

👉 उदाहरण 10: यदि z = 5 + 6i, तो:

रियल भाग = 5
इमेजिनरी भाग = 6

1️⃣1️⃣ सम्मिश्र संख्या का पोलर रूप से कार्टेशियन रूप में परिवर्तन (Polar to Cartesian Conversion)

यदि एक सम्मिश्र संख्या z = r (cos θ + i sin θ) है, तो इसका कार्टेशियन रूप (a + bi) इस प्रकार होगा:

a = r cos θ
b = r sin θ

👉 उदाहरण 1: यदि z = 5 (cos 0.93 + i sin 0.93), तो:

a = 5 cos 0.93 ≈ 3
b = 5 sin 0.93 ≈ 4
तो z = 3 + 4i

1️⃣2️⃣ सम्मिश्र संख्या का कार्टेशियन रूप से पोलर रूप में परिवर्तन (Cartesian to Polar Conversion)

यदि एक सम्मिश्र संख्या z = a + bi है, तो इसका पोलर रूप इस प्रकार होगा:

r = (a² + b²)
θ = tan⁻¹(b/a)

👉 उदाहरण 2: यदि z = 3 + 4i, तो:

r = (3² + 4²) = 5
θ = tan⁻¹(4/3) ≈ 0.93
पोलर रूप: z = 5 (cos 0.93 + i sin 0.93)

1️⃣3️⃣ सम्मिश्र संख्या का De Moivre's Theorem

De Moivre's Theorem के अनुसार, यदि z = r (cos θ + i sin θ) है, तो:

zⁿ = rⁿ [cos(nθ) + i sin(nθ)]

👉 उदाहरण 3: यदि z = 2 (cos 30° + i sin 30°), और n = 3, तो:

z³ = 2³ [cos(90°) + i sin(90°)] = 8i

1️⃣4️⃣ सम्मिश्र संख्याओं का जड़ (Roots of Complex Numbers)

यदि z = r (cos θ + i sin θ) हो, तो z की n जड़ें निम्न प्रकार होंगी:

z_k = r^1/n [cos((θ + 2πk) / n) + i sin((θ + 2πk) / n)]
जहाँ k = 0, 1, 2, ..., n − 1

👉 उदाहरण 4: यदि z = 1 (cos 60° + i sin 60°), और n = 2, तो:

z₀ = 1^1/2 [cos(60° / 2) + i sin(60° / 2)] = cos 30° + i sin 30°
z₁ = 1^1/2 [cos((60° + 360°) / 2) + i sin((60° + 360°) / 2)] = cos 150° + i sin 150°

1️⃣5️⃣ सम्मिश्र संख्याओं का ट्रिगोनोमेट्रिक रूप (Trigonometric Form)

सम्बन्धित ट्रिगोनोमेट्रिक रूप में:

z = r [cos(θ) + i sin(θ)]

👉 उदाहरण 5: यदि z = 3 + 4i, तो:

r = (3² + 4²) = 5
θ = tan⁻¹(4/3) ≈ 0.93
तो ट्रिगोनोमेट्रिक रूप: z = 5 [cos(0.93) + i sin(0.93)]

1️⃣6️⃣ सम्मिश्र संख्याओं का क्यूब (Cube of a Complex Number)

यदि z = a + bi है, तो z का क्यूब निम्नलिखित होगा:

z³ = (a + bi)³ = a³ + 3a²bi + 3ab²i² + b³i³
यहाँ i² = -1 और i³ = -i होता है।

👉 उदाहरण 6: यदि z = 1 + 2i, तो:

z³ = (1 + 2i)³ = 1³ + 3(1²)(2i) + 3(1)(2²)(-1) + (2³)(-i)
z³ = 1 + 6i - 12 - 8i = -11 - 2i

1️⃣7️⃣ सम्मिश्र संख्याओं का नकारात्मक घनमूल (Negative Cube Root)

किसी सम्मिश्र संख्या का नकारात्मक घनमूल निकालने के लिए:

(-z)^1/3 = r^1/3 [cos((θ + 180°) / 3) + i sin((θ + 180°) / 3)]

👉 उदाहरण 7: यदि z = -8, तो:

r = 8, θ = 180°
(-8)^1/3 = 2 [cos(60°) + i sin(60°)]
(-8)^1/3 = 2(1/2 + i3/2) = 1 + i3

4. द्विघात समीकरण (Quadratic Equations)

परिभाषा (Definition):

द्विघात समीकरण वह समीकरण होते हैं जिनमें चर का गुणांक (coefficient) x² के रूप में होता है। इसे सामान्य रूप में इस प्रकार लिखा जाता है:

ax² + bx + c = 0, जहाँ a ≠ 0, और b तथा c किसी भी वास्तविक संख्या हो सकते हैं।

यहाँ:

a: x² का गुणांक (coefficient of x²)
b: x का गुणांक (coefficient of x)
c: एक स्थिरांक (constant)
x: वह चर है जिसे हम हल करना चाहते हैं।

द्विघात समीकरण के प्रकार (Types of Quadratic Equations):

द्विघात समीकरणों के समाधान के लिए विभिन्न विधियाँ होती हैं, जिनमें प्रमुख हैं:

कारक विधि (Factorization Method): जब समीकरण को आसानी से कारकों में विभाजित किया जा सके।
संयोजन विधि (Completing the Square): इस विधि का उपयोग जब समीकरण को पूरा करना हो।
द्विघात समीकरण का सूत्र (Quadratic Formula): यह सबसे सामान्य तरीका है।

द्विघात समीकरण का सूत्र (Quadratic Formula):

द्विघात समीकरण ax² + bx + c = 0 का सामान्य हल निम्नलिखित सूत्र से प्राप्त किया जा सकता है:

x = -b ± b² - 4ac 2a

यहाँ:

Δ = b² - 4ac को विभेद (di/maths-formulas.pngiminant) कहा जाता है।
यदि Δ > 0, तो दो विभिन्न वास्तविक हल होते हैं।
यदि Δ = 0, तो एक वास्तविक हल होता है।
यदि Δ < 0, तो कोई वास्तविक हल नहीं होता, परंतु दो काल्पनिक हल होते हैं।

उदाहरण (Example 1):

प्रश्न: समीकरण x²−5x+6=0 का हल करें।

हल:

यह समीकरण है:

x² - 5x + 6 = 0

यहाँ, a = 1, b = -5, c = 6
विभेद (Δ) = b² - 4ac = (-5)² - 4(1)(6) = 25 - 24 = 1
चूँकि Δ > 0 है, तो हमें दो वास्तविक हल मिलेंगे।
अब, x = -(-5) ± 12(1)
=> x = 5 ± 12
दो हल होंगे:
- x = 5 + 12 = 3
- x = 5 - 12 = 2
उत्तर: समीकरण के हल हैं x = 3 और x = 2।

उदाहरण (Example 2):

प्रश्न: समीकरण 2x² + 3x - 2 = 0 का हल करें।

हल:

यह समीकरण है:

2x² + 3x - 2 = 0

यहाँ, a = 2, b = 3, c = -2
विभेद (Δ) = b² - 4ac = 3² - 4(2)(-2) = 9 + 16 = 25
चूँकि Δ > 0 है, तो दो वास्तविक हल होंगे।
अब, x = -3 ± 252 ( 2 ) -3 ± 25 2(2)
=> x = -3 ± 54
दो हल होंगे:
- x = -3 + 54 = 24 = 0.5
- x = -3 - 54 = -84 = -2
उत्तर: समीकरण के हल हैं x = 0.5 और x = -2।

द्विघात समीकरण के ग्राफ (Graph of Quadratic Equation):

द्विघात समीकरण ax² + bx + c = 0 का ग्राफ एक परबोला (parabola) होता है। यह रेखा x-अक्ष के ऊपर या नीचे हो सकती है, और यह रेखा x-अक्ष को एक बिंदु पर या दो बिंदुओं पर काटती है।

यदि a > 0, तो परबोला x-अक्ष के ऊपर होगा।
यदि a < 0, तो परबोला x-अक्ष के नीचे होगा।
यदि विभेद (Δ) > 0, तो परबोला x-अक्ष को दो बिंदुओं पर काटेगा।
यदि Δ = 0, तो परबोला x-अक्ष को केवल एक बिंदु पर काटेगा।
यदि Δ < 0, तो परबोला x-अक्ष को नहीं काटेगा।

निष्कर्ष (Conclusion):

द्विघात समीकरणों के समाधान के विभिन्न तरीके हैं और ये जीवन की कई समस्याओं में उपयोगी होते हैं। ग्राफ़ द्वारा भी इन समीकरणों को समझना और हल करना आसान होता है। द्विघात समीकरणों का उपयोग कार्यों, वित्तीय गणनाओं, भौतिकी, और कई अन्य क्षेत्रों में किया जाता है।

📚 **अंत में:** इस विषय को अच्छे से समझकर आप किसी भी द्विघात समीकरण को हल कर पाएंगे!

🔹 द्विघात समीकरण के महत्वपूर्ण पहलू 🔹

🔹 समांतर रेखाएँ और उनके गुण:

द्विघात समीकरण का ग्राफ हमेशा एक परबोला (parabola) होता है। यदि दो परबोलas समांतर होते हैं, तो उनका गुणांक एक जैसा होता है। अर्थात, यदि एक समीकरण ax² + bx + c = 0 का ग्राफ और दूसरा समीकरण ax² + bx + c = 0 का ग्राफ समान रेखाएँ होंगे।

🔹 डिस्क्रिमिनेंट (Discriminant):

डिस्क्रिमिनेंट (Δ) एक महत्वपूर्ण मान है जो यह निर्धारित करता है कि द्विघात समीकरण के हल वास्तविक (real) होंगे या काल्पनिक (imaginary)।

डिस्क्रिमिनेंट की परिभाषा: Δ = b² - 4ac

यदि Δ > 0, तो समीकरण के दो वास्तविक और भिन्न हल होंगे।
यदि Δ = 0, तो समीकरण का केवल एक वास्तविक हल होगा।
यदि Δ < 0, तो समीकरण के कोई वास्तविक हल नहीं होंगे, केवल काल्पनिक हल होंगे।

🔹 वर्गमूल (Square Root) विधि:

वर्गमूल विधि का उपयोग उन समीकरणों को हल करने के लिए किया जाता है जिनमें x² के रूप में एक मात्र अज्ञात होता है।

इस विधि में समीकरण को x² = k के रूप में लिखा जाता है और फिर x = ±k से हल किया जाता है।

🔹 समीकरण का निर्धारण और प्रयोग:

द्विघात समीकरण को हल करने के विभिन्न तरीके होते हैं, जैसे:

गुणन विधि (Factorization Method)
वर्गमूल विधि (Square Root Method)
क्वाड्रैटिक फॉर्मूला (Quadratic Formula)

इसके माध्यम से हम किसी भी द्विघात समीकरण को आसानी से हल कर सकते हैं।

🔹 गणना की प्रक्रिया:

द्विघात समीकरणों को हल करने के लिए गणना की प्रक्रिया में निम्नलिखित चरण होते हैं:

समीकरण को सामान्य रूप में लाना (ax² + bx + c = 0)
डिस्क्रिमिनेंट की गणना करें (Δ = b² - 4ac)
हल (Roots) प्राप्त करने के लिए उपयुक्त विधि का चयन करें।

🔹 वर्गीय समीकरणों के ग्राफ:

द्विघात समीकरण का ग्राफ एक परबोला होता है। इसे हम निम्नलिखित प्रकार से समझ सकते हैं:

यदि a > 0, तो परबोला ऊपर की ओर खुलता है।
यदि a < 0, तो परबोला नीचे की ओर खुलता है।

🔹 समीकरणों का गुणन और विभाजन:

द्विघात समीकरणों को गुणन और विभाजन की विधियों से भी हल किया जा सकता है। इस प्रक्रिया में समीकरण को फैक्टरों में विभाजित किया जाता है और फिर उनका गुणन किया जाता है।

उदाहरण: x² - 5x + 6 = 0 को हम (x - 2)(x - 3) = 0 के रूप में फैक्टराइज कर सकते हैं।

🔹 रैखिक असमीकाएँ (Linear Inequalities) 🔹

🔹 रैखिक असमीकाओं की परिभाषा:

रैखिक असमीकाएँ वे असमीकाएँ होती हैं, जिनमें एक रैखिक समीकरण (Linear Equation) के समान किसी वेरिएबल के गुणनफल या योग का तुलना किया जाता है। ये असमीकाएँ वास्तविक संख्याओं से संबंधित होती हैं और इनका रूप निम्नलिखित हो सकता है:

ax + b < c
ax + b > c
ax + b ≤ c
ax + b ≥ c

🔹 रैखिक असमीकाएँ और उनके समाधान:

रैखिक असमीकाएँ उस स्थिति को व्यक्त करती हैं, जब एक रैखिक समीकरण एक विशेष सीमा के भीतर रहता है, जैसे कि किसी वस्तु की कीमतों या किसी अन्य गुणांक के संबंध में। इनका हल एक असमिता रेखा पर रहता है।

🔹 रैखिक असमीकाएँ के प्रकार:

साधारण असमीकाएँ: इनमें एक रैखिक समीकरण के साथ "≤", "≥", "<" या ">" का प्रयोग किया जाता है।
दो चर वाले असमीकाएँ: इसमें दो चर होते हैं, जैसे ax + by ≤ c या ax + by ≥ c।

🔹 समाधान विधि:

रैखिक असमीकाओं को हल करने के दो प्रमुख तरीके होते हैं:

ग्राफिकल विधि: इसमें असमिका को रेखा के रूप में ग्राफ पर चित्रित किया जाता है और असमिता का हल क्षेत्र (region) के रूप में मिलता है।
एल्जेब्राई विधि: इसमें असमिका को समीकरण के रूप में हल किया जाता है और सीमा को निकालकर हल प्राप्त किया जाता है।

🔹 उदाहरण:

उदाहरण 1:

हल करें: 2x + 3 ≤ 7

2x ≤ 7 - 3
2x ≤ 4
x ≤ 2

अतः समाधान x ≤ 2 है।

उदाहरण 2:

हल करें: 3x - 5 > 10

3x > 10 + 5
3x > 15
x > 5

अतः समाधान x > 5 है।

उदाहरण 3:

हल करें: 5x + 4 ≥ 9

5x ≥ 9 - 4
5x ≥ 5
x ≥ 1

अतः समाधान x ≥ 1 है।

🔹 रैखिक असमीकाएँ का ग्राफ:

जब हम रैखिक असमीकाएँ को ग्राफ पर चित्रित करते हैं, तो हमें रेखाएँ मिलती हैं, जो असमिता द्वारा निर्दिष्ट क्षेत्र को दर्शाती हैं। उदाहरण के लिए, यदि हम असमिका 2x + 3 ≤ 7 को चित्रित करें, तो यह एक रेखा होगी और क्षेत्र x ≤ 2 को दर्शाएगा।

🔹 निष्कर्ष:

रैखिक असमीकाएँ गणित में महत्वपूर्ण भूमिका निभाती हैं, विशेष रूप से जब हम वास्तविक दुनिया की समस्याओं को हल करने के लिए उन्हें लागू करते हैं। इनका उपयोग व्यापार, अर्थशास्त्र, और इंजीनियरिंग में भी होता है।

🔹 क्रमचय और संचय (Permutations and Combinations) के सूत्र 🔹

🔹 क्रमचय (Permutations) के सूत्र:

n वस्तुओं का पूर्ण क्रमचय: P(n) = n!
r वस्तुओं का चयन क्रमचय से: P(n, r) = n! / (n - r)!
r वस्तुओं का चयन बिना पुनरावृत्ति के: P(n, r) = n! / (n - r)!

🔹 संचय (Combinations) के सूत्र:

n वस्तुओं में से r वस्तुओं का संचय: C(n, r) = n! / [r!(n - r)!]
r वस्तुओं का चयन बिना क्रम के: C(n, r) = n! / [r!(n - r)!]

🔹 क्रमचय और संचय में अंतर:

क्रमचय: चयन में क्रम को ध्यान में रखा जाता है। उदाहरण के लिए, यदि तीन व्यक्तियों को तीन अलग-अलग स्थानों पर बैठाना है, तो यह क्रमचय होगा।
संचय: चयन में क्रम को नजरअंदाज किया जाता है। उदाहरण के लिए, तीन व्यक्तियों का समूह बनाने में उनका क्रम मायने नहीं रखता।

🔹 उदाहरण:

क्रमचय:

5 व्यक्तियों में से 3 का चयन क्रमचय से: P(5, 3) = 5! / (5 - 3)! = 5! / 2! = 120 / 2 = 60

संचय:

5 व्यक्तियों में से 3 का चयन संचय से: C(5, 3) = 5! / [3!(5 - 3)!] = 5! / (3! * 2!) = 120 / (6 * 2) = 10

🔹 निष्कर्ष:

क्रमचय और संचय गणितीय अवधारणाएँ हैं जो चयन और क्रम से संबंधित समस्याओं को हल करने में उपयोगी होती हैं।

🔹 द्विपद प्रमेय (Binomial Theorem) 🔹

द्विपद प्रमेय के अनुसार, यदि किसी द्विपद (a + b) को किसी घात n तक बढ़ाया जाए, तो उसका विस्तार निम्नलिखित तरीके से होता है:

(a + b)ⁿ = Σ (n C r) a^n-r b^r, जहाँ r = 0 से n तक

यह प्रमेय द्विपद का विस्तार करने के लिए प्रयोग किया जाता है। 🔍

🔹 पाइथागोरस प्रमेय (Pythagorean Theorem) 🔹

पाइथागोरस प्रमेय त्रिकोणमिति के एक महत्वपूर्ण प्रमेय है। यदि किसी समकोण त्रिकोण के दो लम्बे पक्षों की लंबाइयाँ a और b हैं, और कर्ण की लंबाई c है, तो यह निम्नलिखित होता है:

c² = a² + b²

🔹 त्रिकोणमिति प्रमेय (Trigonometric Identities) 🔹

त्रिकोणमिति के प्रमेय बहुत उपयोगी होते हैं। कुछ महत्वपूर्ण प्रमेय निम्नलिखित हैं:

sin²θ + cos²θ = 1 ✅
1 + tan²θ = sec²θ 🌟
1 + cot²θ = cosec²θ 🔥
sin(θ) = 1/cosec(θ), cos(θ) = 1/sec(θ), tan(θ) = 1/cot(θ)

🔹 संख्याओं का गुणनफल (Product of Numbers) 🔹

संख्याओं के गुणनफल से संबंधित कुछ प्रमेय:

a × b = b × a (गुणन का प्रतिस्थापन गुण) 🔄
(a × b) × c = a × (b × c) (गुणन में संघटन गुण) 🔗
a × (b + c) = a × b + a × c (वितरण गुण) 📊

🔹 वर्गमूल प्रमेय (Square Root Theorem) 🔹

वर्गमूल से संबंधित प्रमेय:

(a × b) = a × b 🔀
(a / b) = a / b ➗
(a²) = |a| (किसी संख्या का वर्गमूल उसका परिमाण होता है) 💡

🔹 संख्याओं का जोड़ (Sum of Numbers) 🔹

संख्याओं के जोड़ से संबंधित प्रमेय:

समीकरण का जोड़: a + b = b + a (जोड़ का प्रतिस्थापन गुण) 🔄
यदि x = y और y = z, तो x = z (समानता का गुण) ✅

🔹 असमानता प्रमेय (Inequality Theorem) 🔹

असमानता से संबंधित कुछ प्रमेय:

यदि a > b और b > c, तो a > c (असमानता का गुण) ➡️
यदि a ≤ b और b ≤ c, तो a ≤ c 🔻
|a + b| ≤ |a| + |b| (त्रिकोण असमानता) ⛔

🔹 गणना सूत्र (Calculation Formulas) 🔹

गणना से संबंधित प्रमेय और सूत्र:

साधारण ब्याज: I = P × R × T / 100 💸
संयोजन: n C r = n! / (r!(n - r)!) 📊
पिरामिड का आयतन: V = (1/3) × B × h (जहाँ B = आधार क्षेत्रफल, h = ऊँचाई) 🏰

🔹 गणितीय श्रृंखला (Mathematical Series) 🔹

गणितीय श्रृंखला से संबंधित कुछ प्रमेय:

समीकरण Σ a_n (संपूर्ण श्रृंखला) की प्राप्ति के लिए उपयोगी है 🔄
संपूर्ण संख्या जोड़: S = n/2 [2a + (n - 1)d] 📈
गणितीय श्रृंखला का योग: S = n/2 [a + l] 🔑

🔹 गणितीय सांख्यिकी प्रमेय (Mathematical Statistics Theorems) 🔹

गणितीय सांख्यिकी से संबंधित प्रमेय:

औसत (Mean) = Σx / n 🔄
विविधता (Variance) = Σ(x - mean)² / n 📏
सांख्यिकी औसत: μ = Σ(x × P(x)) 📐

🔹 द्विपद प्रमेय (Binomial Theorem) 🔹

यह प्रमेय द्विपद का विस्तार करने के लिए प्रयोग किया जाता है।

(a + b)ⁿ = Σ (n C r) a^n-r b^r, जहाँ r = 0 से n तक

🔹 पाइथागोरस प्रमेय (Pythagorean Theorem) 🔹

यदि किसी समकोण त्रिकोण के दो लम्बे पक्षों की लंबाइयाँ a और b हैं, और कर्ण की लंबाई c है, तो यह निम्नलिखित होता है:

c² = a² + b²

🔹 अनुक्रम और श्रेणी (Sequence and Series) 🔹

🔹 अनुक्रम (Sequence):

अनुक्रम एक संख्या या वस्तुओं का अनुशासित क्रम होता है, जिसे आमतौर पर a₁, a₂, a₃, ... के रूप में दर्शाया जाता है। यहाँ हर संख्या एक स्थान (term) होती है और अनुक्रम के लिए स्थानों का क्रम महत्त्वपूर्ण होता है।

उदाहरण: 1, 3, 5, 7, 9, ... यह एक अनुक्रम है जिसमें प्रत्येक स्थान पर एक संख्या दी गई है।
अनुक्रम के प्रकार:
- समानांतर अनुक्रम (Arithmetic Sequence): यह अनुक्रम ऐसा होता है जिसमें प्रत्येक स्थान के बीच समान अंतर होता है।
- ज्यामितीय अनुक्रम (Geometric Sequence): यह अनुक्रम ऐसा होता है जिसमें प्रत्येक स्थान के बीच समान गुणा (common ratio) होता है।

🔹 समानांतर अनुक्रम (Arithmetic Sequence):

समानांतर अनुक्रम वह होता है जिसमें हर दो अनुक्रम के बीच समान अंतर होता है। इसे सामान्यतः a₁, a₂, a₃, ... के रूप में लिखा जाता है, जहाँ हर स्थान का अंतर (common difference) समान होता है।

समानांतर अनुक्रम का सामान्य रूप:
a_n = a₁ + (n - 1)d
जहाँ, a₁ = पहले स्थान की संख्या, d = अंतर (common difference), n = स्थान का नंबर।

🔹 ज्यामितीय अनुक्रम (Geometric Sequence):

ज्यामितीय अनुक्रम वह अनुक्रम है जिसमें हर दो स्थानों के बीच समान गुणा (common ratio) होता है। इसका सामान्य रूप है:

ज्यामितीय अनुक्रम का सामान्य रूप:
a_n = a₁ × r^n-1
जहाँ, a₁ = पहले स्थान की संख्या, r = गुणा (common ratio), n = स्थान का नंबर।

🔹 श्रेणी (Series):

श्रेणी वह गणना होती है जो किसी अनुक्रम के स्थानों को जोड़ने पर प्राप्त होती है। अर्थात, यदि हमारे पास अनुक्रम a₁, a₂, a₃, ... है, तो उस अनुक्रम की श्रेणी होगी:

श्रेणी का सामान्य रूप:
S_n = a₁ + a₂ + a₃ + ... + a_n

🔹 समानांतर श्रेणी (Arithmetic Series):

समानांतर श्रेणी वह होती है जो समानांतर अनुक्रम के स्थानों का योग होती है। इसका सामान्य रूप होता है:

समानांतर श्रेणी का योग:
S_n = n/2 × (2a₁ + (n - 1)d)
जहाँ, n = संख्या के स्थानों की संख्या, a₁ = पहले स्थान की संख्या, d = अंतर (common difference)।

🔹 ज्यामितीय श्रेणी (Geometric Series):

ज्यामितीय श्रेणी वह होती है जो ज्यामितीय अनुक्रम के स्थानों का योग होती है। इसका सामान्य रूप होता है:

ज्यामितीय श्रेणी का योग:
S_n = a₁ × (1 - rⁿ) / (1 - r), यदि |r| < 1 हो।
जहाँ, a₁ = पहले स्थान की संख्या, r = गुणा (common ratio), n = स्थानों की संख्या।

🔹 उदाहरण:

समानांतर अनुक्रम का उदाहरण:

यदि a₁ = 2 और d = 3 हो, तो पहले 5 स्थानों की समानांतर अनुक्रम की श्रेणी का योग होगा:

S₅ = 5/2 × (2 × 2 + (5 - 1) × 3) = 5/2 × (4 + 12) = 5/2 × 16 = 40

ज्यामितीय अनुक्रम का उदाहरण:

यदि a₁ = 3 और r = 2 हो, तो पहले 4 स्थानों का ज्यामितीय अनुक्रम होगा:

S₄ = 3 × (1 - 2⁴) / (1 - 2) = 3 × (1 - 16) / (-1) = 3 × (-15) / (-1) = 45

🔹 अनंत श्रेणी (Infinite Series):

जब किसी श्रेणी में अनंत संख्या के स्थान होते हैं, तो वह अनंत श्रेणी कहलाती है। ऐसे ज्यामितीय श्रेणियाँ जहां | r | < 1 हो, उनका योग किया जा सकता है:

अनंत ज्यामितीय श्रेणी का योग:
S = a₁ / (1 - r), जहाँ | r | < 1।

🔹 उदाहरण:

अनंत ज्यामितीय श्रेणी का उदाहरण:

यदि a₁ = 5 और r = 1/2 हो, तो श्रेणी का योग होगा:

S = 5 / (1 - 1/2) = 5 / (1/2) = 10

🔹 उपयोग:

समानांतर अनुक्रम और श्रेणी का उपयोग गणना, रेट्स, और निश्चित राशि की भविष्यवाणी में किया जाता है।
ज्यामितीय अनुक्रम का उपयोग निवेश की वृद्धि, मापने की प्रक्रिया और धारा की अनुपातों के गणनाओं में होता है।

🔹 सरल रेखाएँ (Straight Lines) के Formulas 🔹

🔹 साधारण रूप (General Form) 🔹

Ax + By + C = 0

Example: 2x + 3y - 5 = 0 का ढाल और अवरोध ज्ञात करें।

Solution:
साधारण रूप: 2x + 3y - 5 = 0
ढाल (Slope) = -A/B = -2/3
x-अवरोध: y = 0 रखने पर, 2x - 5 = 0 ⇒ x = 5/2
y-अवरोध: x = 0 रखने पर, 3y - 5 = 0 ⇒ y = 5/3

🔹 ढाल (Slope) 🔹

m = -A/B

Example: रेखा 4x + 5y + 7 = 0 की ढाल ज्ञात करें।

Solution:
A = 4, B = 5
m = -A/B = -4/5

🔹 दो बिंदुओं से गुजरने वाली रेखा 🔹

(y - y₁) = y₂ - y₁x₂ - x₁(x - x₁)

Example: बिंदु (2, 3) और (4, 7) से गुजरने वाली रेखा का समीकरण ज्ञात करें।

Solution:
x₁ = 2, y₁ = 3, x₂ = 4, y₂ = 7
ढाल (m) = (7 - 3)/(4 - 2) = 4/2 = 2
समीकरण: (y - 3) = 2(x - 2)
⇒ y - 3 = 2x - 4
⇒ 2x - y - 1 = 0

🔹 ढाल-बिंदु रूप (Slope-Point Form) 🔹

(y - y₁) = m(x - x₁)

Example: ढाल 3 और बिंदु (1,2) के लिए रेखा का समीकरण लिखो।

Solution:
m = 3, (x₁, y₁) = (1, 2)
समीकरण: (y - 2) = 3(x - 1)
⇒ y - 2 = 3x - 3
⇒ 3x - y - 1 = 0

🔹 अवरोध रूप (Intercept Form) 🔹

xa + yb = 1

Example: x-अवरोध = 3, y-अवरोध = 4 वाली रेखा का समीकरण लिखिए।

Solution:
a = 3, b = 4
समीकरण: x/3 + y/4 = 1
⇒ 4x + 3y = 12

🔹 दो रेखाओं के बीच कोण 🔹

tanθ = (m₂ - m₁)/(1 + m₁m₂)

Example: दो रेखाएँ जिनकी ढालें m₁ = 1, m₂ = 2 हों, उनके बीच का कोण ज्ञात करें।

Solution:
m₁ = 1, m₂ = 2
tanθ = (2 - 1)/(1 + (1)(2)) = 1/3
θ = tan^-1(1/3)

🔹 बिंदु से रेखा तक दूरी 🔹

d = |Ax₁ + By₁ + C| / (A² + B²)

Example: बिंदु (2,3) से रेखा 3x + 4y - 5 = 0 तक दूरी ज्ञात करें।

Solution:
A = 3, B = 4, C = -5
x₁ = 2, y₁ = 3
दूरी: d = |3×2 + 4×3 - 5| / (3² + 4²)
⇒ d = |6 + 12 - 5| / (9 + 16)
⇒ d = |13| / 25
⇒ d = 13/5 = 2.6

🔹 दो समांतर रेखाओं के बीच दूरी 🔹

d = |C₂ - C₁| / (A² + B²)

Example: रेखाएँ 3x + 4y - 5 = 0 और 3x + 4y + 7 = 0 के बीच दूरी ज्ञात करें।

Solution:
A = 3, B = 4, C₁ = -5, C₂ = 7
d = |7 - (-5)| / (3² + 4²)
d = |12| / (9 + 16)
d = 12/5 = 2.4

🔹 समवर्ती रेखाएँ (Concurrent Lines) 🔹

तीनों रेखाओं का निर्धारण एक ही बिंदु से होता है।

Example: दिखाइए कि रेखाएँ x + y - 5 = 0, 2x - y + 1 = 0 और x - 3y + 7 = 0 समवर्ती हैं।

Solution:
पहले दो रेखाओं को हल करें: x + y = 5 और 2x - y = -1
दोनों जोड़ने पर: 3x = 4 ⇒ x = 4/3
फिर x = 4/3 रखने पर y = 11/3
अब तीसरी रेखा में (4/3, 11/3) रखने पर जाँच करें।
x - 3y + 7 = (4/3) - 3(11/3) + 7 = 0
अतः तीनों रेखाएँ समवर्ती हैं।

🔹 रेखा की सामान्य दूरी (Normal Form of Line) 🔹

x cosθ + y sinθ = p

Example: रेखा 3x + y = 2 को Normal Form में लिखिए।

Solution:
3x + y - 2 = 0
Comparing with Ax + By + C = 0
Normalize: Divide by (A² + B²)
( √(3)² + 1² )= (3 + 1) = 2
New equation: (3/2)x + (1/2)y = 1

🔹 दो रेखाओं का समकोणता (Perpendicular Lines) 🔹

m₁ × m₂ = -1

Example: यदि पहली रेखा की ढाल 2 है, तो दूसरी समकोण रेखा की ढाल ज्ञात करें।

Solution:
m₁ = 2
m₂ = -1/2
क्योंकि m₁ × m₂ = 2 × (-1/2) = -1

🔹 एक बिंदु से जाने वाली रेखाएँ 🔹

Equation: y - y₁ = m(x - x₁)

Example: बिंदु (2,3) से ढाल 4 वाली रेखा का समीकरण लिखो।

Solution:
m = 4
Equation: (y - 3) = 4(x - 2)
⇒ y - 3 = 4x - 8
⇒ 4x - y - 5 = 0

🔹 दो रेखाओं का समांतरता (Parallel Lines) 🔹

m₁ = m₂

Example: रेखा 2x - 3y + 7 = 0 के समांतर रेखा का समीकरण लिखिए जो (1,2) से गुजरती हो।

Solution:
Given line: 2x - 3y + 7 = 0, slope m = 2/3
Equation: (y - 2) = (2/3)(x - 1)
⇒ 3(y - 2) = 2(x - 1)
⇒ 3y - 6 = 2x - 2
⇒ 2x - 3y + 4 = 0

🔹 रेखा का ढाल एवं अवरोध रूप 🔹

y = mx + c

Example: ढाल 3 और y-अवरोध 5 वाली रेखा का समीकरण लिखिए।

Solution:
m = 3, c = 5
Equation: y = 3x + 5

🔹 दो रेखाओं के मिलने का बिंदु 🔹

दोनों रेखाओं को हल करके (x,y) प्राप्त करें।

Example: रेखाएँ x + y = 5 और x - y = 1 का मिलन बिंदु ज्ञात करें।

Solution:
Equation 1: x + y = 5
Equation 2: x - y = 1
दोनों जोड़ें: 2x = 6 ⇒ x = 3
x = 3 रखने पर y = 2
मिलन बिंदु (3,2)

🔹 खंड फलन (Section Formula) 🔹

(mx₂ + nx₁) / (m+n), (my₂ + ny₁) / (m+n)

Example: बिंदु (2,3) और (4,7) को अनुपात 2:3 में विभाजित करने वाले बिंदु के निर्देशांक ज्ञात करें।

Solution:
m:n = 2:3
x = (2×4 + 3×2)/(2+3) = (8+6)/5 = 14/5 = 2.8
y = (2×7 + 3×3)/(2+3) = (14+9)/5 = 23/5 = 4.6
बिंदु (2.8, 4.6)

शंकवक्र (Conic Sections)

1️⃣ वृत्त (Circle)

(x - h)² + (y - k)² = r²

उदाहरण : केंद्र (2, 3) और त्रिज्या 5 वाले वृत्त का समीकरण ज्ञात कीजिए।

समाधान :
केंद्र (h, k) = (2, 3), त्रिज्या (r) = 5 है।
वृत्त का सामान्य रूप: (x - h)² + (y - k)² = r²
मान स्थापित करें: (x - 2)² + (y - 3)² = 5²
5 का वर्ग = 25 होता है।
अतः समीकरण होगा: (x - 2)² + (y - 3)² = 25

2️⃣ परवलय (Parabola)

y² = 4ax या x² = 4ay

उदाहरण : यदि शीर्ष (Vertex) मूल बिंदु (0,0) पर है और फोकस (2,0) पर है, तो परवलय का समीकरण ज्ञात कीजिए।

समाधान :
चूंकि फोकस x-अक्ष पर है, इसलिए परवलय का रूप होगा: y² = 4ax
यहाँ, a = 2
मान स्थापित करें: y² = 4 × 2 × x = 8x
अतः परवलय का समीकरण होगा: y² = 8x

🔥 परवलय (Parabola) की Tricks

1️⃣ यदि रूप हो: y² = 4ax

भुजा: x-अक्ष के समानांतर (right side खुला)
फोकस: (a, 0)
डायरेक्ट्रिक्स: x = -a
मुख्य अक्ष: x-अक्ष

2️⃣ यदि रूप हो: y² = -4ax

भुजा: x-अक्ष के समानांतर (left side खुला)
फोकस: (-a, 0)
डायरेक्ट्रिक्स: x = a
मुख्य अक्ष: x-अक्ष

3️⃣ यदि रूप हो: x² = 4ay

भुजा: y-अक्ष के समानांतर (ऊपर की ओर खुला)
फोकस: (0, a)
डायरेक्ट्रिक्स: y = -a
मुख्य अक्ष: y-अक्ष

4️⃣ यदि रूप हो: x² = -4ay

भुजा: y-अक्ष के समानांतर (नीचे की ओर खुला)
फोकस: (0, -a)
डायरेक्ट्रिक्स: y = a
मुख्य अक्ष: y-अक्ष

3️⃣ दीर्घवृत्त (Ellipse)

x²y² + y²b² = 1

उदाहरण : केंद्र मूल बिंदु पर स्थित एक दीर्घवृत्त का समीकरण ज्ञात कीजिए, जहाँ a = 5 और b = 3 है।

समाधान :
दीर्घवृत्त का सामान्य रूप: (x² / a²) + (y² / b²) = 1
यहाँ a = 5 और b = 3 है।
मान स्थापित करें: (x² / 25) + (y² / 9) = 1
अतः दीर्घवृत्त का समीकरण होगा: (x² / 25) + (y² / 9) = 1

4️⃣ अतिपरवलय (Hyperbola)

x²y² - y²b² = 1

उदाहरण : केंद्र मूल बिंदु पर स्थित एक अतिपरवलय का समीकरण ज्ञात कीजिए, जहाँ a = 4 और b = 3 है।

समाधान :
अतिपरवलय का सामान्य रूप: (x² / a²) - (y² / b²) = 1
यहाँ a = 4 और b = 3 है।
मान स्थापित करें: (x² / 16) - (y² / 9) = 1
अतः अतिपरवलय का समीकरण होगा: (x² / 16) - (y² / 9) = 1

5️⃣ फोकस (Focus) के फार्मूले

परवलय का फोकस : (a, 0) या (0, a) दीर्घवृत्त का फोकस : (±c, 0) या (0, ±c) अतिपरवलय का फोकस : (±c, 0) या (0, ±c)

उदाहरण:

👉 परवलय y² = 8x का फोकस ज्ञात करें।

Solution:
परवलय y² = 4ax के रूप में है।
यहाँ 4a = 8 ⇒ a = 2
तो फोकस होगा (2, 0)

6️⃣ डायरेक्ट्रिक्स (निर्देश रेखा) के फार्मूले

परवलय की डायरेक्ट्रिक्स : x = -a या y = -a दीर्घवृत्त की डायरेक्ट्रिक्स : x = ±a/e या y = ±a/e अतिपरवलय की डायरेक्ट्रिक्स : x = ±a/e या y = ±a/e

उदाहरण:

👉 परवलय y² = 8x की डायरेक्ट्रिक्स ज्ञात करें।

Solution:
परवलय का सामान्य रूप y² = 4ax होता है।
यहाँ a = 2 है।
तो निर्देश रेखा का समीकरण होगा x = -2

7️⃣ अक्ष (Axis of Symmetry) के फार्मूले

परवलय का अक्ष : x-axis या y-axis के समानांतर दीर्घवृत्त का अक्ष : मुख्य अक्ष व लघु अक्ष अतिपरवलय का अक्ष : x-axis या y-axis

उदाहरण:

👉 परवलय y² = 8x का अक्ष ज्ञात करें।

Solution:
यह y² है ⇒ अक्ष x-axis के समानांतर है।

8️⃣ पार्श्व अक्ष (Latus Rectum) के फार्मूले

परवलय का पार्श्व अक्ष = 4a दीर्घवृत्त का पार्श्व अक्ष = (2b²)/a अतिपरवलय का पार्श्व अक्ष = (2b²)/a

उदाहरण:

👉 परवलय y² = 8x का पार्श्व अक्ष ज्ञात करें।

Solution:
4a = 8 ⇒ a = 2
तो पार्श्व अक्ष = 4a = 8 इकाई

9️⃣ शीर्ष (Vertex) के फार्मूले

सभी शंकवक्रों में सामान्यतः Vertex : (0,0) होता है। अगर खिसकाया जाए तो (h, k) हो सकता है।

उदाहरण:

👉 परवलय (y - 2)² = 8(x + 3) का शीर्ष ज्ञात करें।

Solution:
सामान्य रूप (y - k)² = 4a(x - h) है।
यहाँ h = -3 और k = 2
तो शीर्ष (Vertex) है (-3, 2)

त्रिविमीय ज्यामिति (Three Dimensional Geometry) के मुख्य सूत्र

🔹 1. दो बिंदुओं के बीच की दूरी का सूत्र

d = ((x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²)

जहाँ (x₁, y₁, z₁) और (x₂, y₂, z₂) दो बिंदु हैं।

🔹 2. दो बिंदुओं के मध्य बिंदु (Midpoint) का सूत्र

M = ((x₁ + x₂)2, (y₁ + y₂)2, (z₁ + z₂)2)

🔹 3. किसी बिंदु से अक्षों तक दूरी

यदि कोई बिंदु (x, y, z) है, तो:

O से X-अक्ष तक दूरी = (y² + z²)
O से Y-अक्ष तक दूरी = (x² + z²)
O से Z-अक्ष तक दूरी = (x² + y²)

🔹 4. रेखा का सदिश (Vector) और कार्तीय समीकरण

सदिश रूप:
r = a + λb

जहाँ a = स्थिति सदिश (Position Vector) और b = दिशा सदिश (Direction Vector) होता है।

कार्तीय रूप:
(x - x₁)a = (y - y₁)b = (z - z₁)c

🔹 5. दो रेखाओं के बीच की कोण (Angle between two lines)

cos θ = (a₁a₂ + b₁b₂ + c₁c₂) / ((a₁² + b₁² + c₁²) (a₂² + b₂² + c₂²))

🔹 6. समतल (Plane) का सामान्य समीकरण

Ax + By + Cz + D = 0

जहाँ (A, B, C) समतल का सामान्य सदिश (Normal Vector) है।

🔹 7. समतल का सदिश समीकरण

r . n = d

जहाँ n = समतल का सामान्य सदिश और d = समतल से मूल बिंदु तक लम्ब दूरी।

🔹 8. बिंदु और समतल के बीच की दूरी

D = |Ax₁ + By₁ + Cz₁ + D| / (A² + B² + C²)

🔹 9. दो समतलों के बीच का कोण (Angle between two planes)

cos θ = (A₁A₂ + B₁B₂ + C₁C₂) / ((A₁² + B₁² + C₁²) (A₂² + B₂² + C₂²))

🔹 10. रेखा और समतल के बीच का कोण

sin θ = (A a + B b + C c) / ((A² + B² + C²) (a² + b² + c²))

जहाँ (a, b, c) रेखा का दिशा अनुपात (Direction Ratio) होता है।

त्रिविमीय ज्यामिति (Three Dimensional Geometry) के अतिरिक्त सूत्र

🔹 11. रेखा और समतल का परस्पर अनुपाती (Line and Plane Intersection)

r = a + λb

जहाँ r = रेखा का सामान्य समीकरण, a = स्थिति सदिश (position vector), b = दिशा सदिश (direction vector), λ = स्केलर गुणांक।

🔹 12. रेखा और समतल के बीच की न्यूनतम दूरी (Minimum Distance Between Line and Plane)

D = |(r₀ - r₁) . n| / |n|

यहाँ r₀ = बिंदु पर समतल, r₁ = रेखा पर बिंदु, n = समतल का सामान्य सदिश।

🔹 13. त्रिविमीय समतल का सामान्य समीकरण (General Equation of a Plane in Three Dimensional Space)

Ax + By + Cz + D = 0

यह समतल का सामान्य रूप है, जहाँ (A, B, C) समतल का सामान्य सदिश है।

🔹 14. समतल और बिंदु के बीच की दूरी

D = |Ax₁ + By₁ + Cz₁ + D| / (A² + B² + C²)

यहाँ (x₁, y₁, z₁) बिंदु का स्थान है और (A, B, C) समतल का सामान्य सदिश है।

🔹 15. बिंदु और समतल के बीच लम्ब दूरी

D = |(x₁, y₁, z₁) . (a, b, c)| / (a² + b² + c²)

यह बिंदु (x₁, y₁, z₁) और समतल का सामान्य समीकरण है।

🔹 16. रेखा और समतल के बीच लम्ब दूरी

D = |(r₀ - r₁) . n| / (n₁² + n₂² + n₃²)

यहाँ r₀ = समतल का बिंदु, r₁ = रेखा का बिंदु, n = समतल का सामान्य सदिश है।

🔹 17. दो समतलों के बीच का कोण (Angle between two planes)

cos θ = (A₁A₂ + B₁B₂ + C₁C₂) / (A₁² + B₁² + C₁²) (A₂² + B₂² + C₂²)

यहाँ A₁, B₁, C₁ और A₂, B₂, C₂ समतल का सामान्य सदिश है।

🔹 18. त्रिविमीय शंकु का समीकरण

z² = x² + y²

यह त्रिविमीय शंकु (Cone) का समीकरण है।

🔹 19. त्रिविमीय शंकु का लंबवत तल (Vertical Slice of a Cone)

y² = 4ax

यह त्रिविमीय शंकु का समीकरण है जहाँ a शंकु का आकार निर्धारित करता है।

🔷 सीमाएँ (Limits) के सभी महत्त्वपूर्ण सूत्र

🔷 1. Algebraic Limits (बीजगणितीय सीमाएँ)

सूत्र	मान
lim_x→a xⁿ	aⁿ
lim_x→a (x - a)	0
lim_x→a xⁿ - aⁿx - a	n × a^{n - 1}
lim_x→0 (1 + x)ⁿ - 1x	n
lim(x + y - z)	lim x + lim y - lim z
lim(xyz)	lim x × lim y × lim z
lim(xy)	lim xlim y

🔷 2. Trigonometric Limits (त्रिकोणमितीय सीमाएँ)

सूत्र	मान
lim_x→0 sin xx	1
lim_x→0 tan xx	1
lim_x→0 1 - cos xx²	12
lim_x→0 sin(ax)bx	ab

🔷 3. Limits at Infinity (अनंत पर सीमाएँ)

सूत्र	मान
lim_x→∞ 1x	0
lim_x→∞ 1xⁿ (n > 0)	0
lim_x→∞ xx + 1	1
lim_x→∞ axⁿ + ...bxⁿ + ...	ab

🔷 4. Continuity and Limits (सातत्य और सीमाएँ)

कथन	स्थिति
यदि lim_x→a f(x) = f(a)	तो f(x) निरंतर है (Continuous at x = a)
यदि Left-hand limit = Right-hand limit = f(a)	तो f(x) निरंतर है

🔷 5. Left-hand और Right-hand Limits

प्रकार	परिभाषा
Left-hand Limit (LHL)	lim_x→a⁻ f(x)
Right-hand Limit (RHL)	lim_x→a⁺ f(x)
यदि LHL = RHL	तो limit मौजूद (exists)

🔷 6. Standard Limit Formulas (मानक सीमा सूत्र)

Function	Limit
lim(x + y - z)	lim x + lim y - lim z
lim(xyz)	lim x × lim y × lim z
lim(xy)	lim xlim y
lim[Cf(x)]	C × lim[f(x)]
lim[f(x)]ⁿ	(lim[f(x)])ⁿ
lim e^x	∞
lim e^-x	0
lim ln x (x → 0⁺)	-∞
lim xⁿ (x → 0, n > 0)	0
lim xx!	0
lim (1 + kx)^x	e^k, (e = 2.71)
lim (1 - 1x)^x	1e
lim (x^x e^-x)	2π
lim log_a(1 + 1x)	log_a e
lim log_e(1+x)x	1
lim xsin x	1
lim xtan x	1
lim 1 - cos xx	0
lim 1 - cos xx²	12

Trigonometric Limits at Different Angles

Angle (θ)	lim (sin θ)	lim (cos θ)	lim (tan θ)	lim (cot θ)	lim (sec θ)	lim (csc θ)
θ → 0	0	1	0	∞	1	∞
θ → π/2 (90°)	1	0	∞	0	∞	1
θ → π (180°)	0	-1	0	-∞	-1	-∞
θ → 3π/2 (270°)	-1	0	-∞	0	-∞	-1

Derivatives (अवकलज) के सभी जरूरी टॉपिक्स और फार्मूले

1. प्रथम सिद्धांत द्वारा अवकलज (First Principle)

f(x) का अवकलज:
Solution-

f'(x) = f(x + h) − f(x)h, जहाँ h → 0

2. बहुपद फलनों का अवकलज (Polynomial Functions)

Formula-

ddx(xⁿ) = n·xⁿ⁻¹

3. गुणन नियम (Product Rule)

Formula-

ddx[f(x)·g(x)] = f'(x)·g(x) + f(x)·g'(x)

4. भाजन नियम (Quotient Rule)

Formula-

ddxf(x)g(x) = f'(x)·g(x) − f(x)·g'(x)g(x)²

5. श्रृंखला नियम (Chain Rule)

Formula-

dydx = dydu × dudx

6. लघुगणकीय फलनों का अवकलज (Logarithmic Functions)

Formulas-
- ddx(ln x) = 1x
- ddx(log_ax) = 1x·ln a

7. घातांक फलनों का अवकलज (Exponential Functions)

Formulas-
- ddx(e^x) = e^x
- ddx(a^x) = a^x·ln a

8. त्रिकोणमितीय फलनों का अवकलज (Trigonometric Functions)

Formulas-
- ddx(sin x) = cos x
- ddx(cos x) = −sin x
- ddx(tan x) = sec²x
- ddx(cot x) = −csc²x
- ddx(sec x) = sec x·tan x
- ddx(csc x) = −csc x·cot x

9. व्युत्क्रम त्रिकोणमितीय फलनों का अवकलज (Inverse Trigonometric Functions)

Formulas-
- ddx(sin⁻¹x) = 1(1 − x²)
- ddx(cos⁻¹x) = − 1(1 − x²)
- ddx(tan⁻¹x) = 11 + x²

10. उच्च कोटि के अवकलज (Higher Order Derivatives)

Definition-

f''(x) = d²dx² f(x)

f⁽ⁿ⁾(x) = dⁿdxⁿ f(x)

11. निहित अवकलन (Implicit Differentiation)

Example- यदि x² + y² = 1

तो dydx = −xy

12. मूलों वाले फलनों का अवकलज (Functions Involving Roots)

Formula-

ddx(g(x)) = g'(x)2g(x)

13. पैरामीट्रिक अवकलन (Parametric Differentiation)

Formula-

यदि x = f(t), y = g(t), तब:

dydx = dy/dtdx/dt

📘 कक्षा 11 सांख्यिकी: सभी महत्वपूर्ण सूत्र

1. वर्ग की चौड़ाई (Class Width)

वर्ग की चौड़ाई = अधिकतम मान − न्यूनतम मानवर्गों की संख्या

2. वर्ग मध्य (Class Midpoint)

वर्ग मध्य = निम्न सीमा + उच्च सीमा2

3. माध्य (Mean)

असंग्रहीत आंकड़े: Σxn
समूहित आंकड़े: Σf·xΣf

4. माध्यिका (Median)

Median = L + N2 − CF f × h

जहाँ:

L = माध्यिका वर्ग की निम्न सीमा
N = कुल आवृत्ति
CF = माध्यिका वर्ग से पहले की संचयी आवृत्ति
f = माध्यिका वर्ग की आवृत्ति
h = वर्ग की चौड़ाई

5. बहुलक (Mode)

Mode = L + (f₁ − f₀) 2f₁ − f₀ − f₂ × h

जहाँ:

L = बहुलक वर्ग की निम्न सीमा
f₁ = बहुलक वर्ग की आवृत्ति
f₀ = बहुलक वर्ग से पहले वर्ग की आवृत्ति
f₂ = बहुलक वर्ग के बाद के वर्ग की आवृत्ति
h = वर्ग की चौड़ाई

6. औसत विचलन (Mean Deviation)

माध्य के सापेक्ष: MD = Σ|x − x̄|n
माध्यिका के सापेक्ष: MD = Σ|x − M|n

7. मानक विचलन (Standard Deviation)

असंग्रहीत आंकड़े: σ = Σ(x − x̄)²n
समूहित आंकड़े: σ = Σf(x − x̄)²Σf

8. प्रसरण (Variance)

असंग्रहीत आंकड़े: σ² = Σ(x − x̄)²n
समूहित आंकड़े: σ² = Σf(x − x̄)²Σf

9. प्रसरण गुणांक (Coefficient of Variation)

CV = σx̄ × 100%

10. श्रृंखला का संयोजन (Combined Mean)

Combined Mean = n₁x̄₁ + n₂x̄₂n₁ + n₂

11. रेंज (Range)

Range = अधिकतम मान − न्यूनतम मान

12. क्वारटाइल विचलन (Quartile Deviation)

Q.D. = Q₃ − Q₁2

13. क्वारटाइल विचलन गुणांक (Coefficient of Quartile Deviation)

Coefficient = Q₃ − Q₁Q₃ + Q₁

14. माध्य विचलन गुणांक (Coefficient of Mean Deviation)

Coefficient = MDx̄

15. मानक विचलन गुणांक (Coefficient of Standard Deviation)

Coefficient = σx̄

16. समांतर माध्य (Assumed Mean Method)

Mean = a + ΣfdΣf

जहाँ:

a = अनुमानित माध्य
d = x − a

17. चरण विचलन विधि (Step Deviation Method)

Mean = a + ΣfuΣf × h

जहाँ:

u = x − ah
h = वर्ग की चौड़ाई

18. माध्य, माध्यिका और बहुलक के बीच संबंध

Mode = 3 × Median − 2 × Mean

📌 यह टॉपिक आपकी कक्षा 9वीं में भी दिया गया है। और अधिक जानने के लिए यहाँ क्लिक करें।

कक्षा 11 के लिए प्रायिकता (Probability) के सभी जरूरी सूत्र

1. प्रायिकता का सिद्धांत (Basic Probability Theory)

प्रायिकता = (सफलता की संख्या) / (सभी संभावनाओं की संख्या)
P(E) = ईवेंट E की प्रायिकता
P(S) = 1 (कुल संभावनाओं का योग हमेशा 1 होता है)

2. कंप्लीमेंटरी प्रायिकता (Complementary Probability)

P(E') = 1 − P(E) (जहां P(E') = ईवेंट E का पूरक)

3. जोड़ नियम (Addition Law)

P(A ∪ B) = P(A) + P(B) − P(A ∩ B)
यदि A और B परस्पर अनन्य (Mutually Exclusive) हैं, तो:
- P(A ∪ B) = P(A) + P(B)

4. गुणन नियम (Multiplication Law)

P(A ∩ B) = P(A) × P(B | A) (Conditional Probability)
यदि A और B स्वतंत्र हैं, तो:
- P(A ∩ B) = P(A) × P(B)

5. शर्तीय प्रायिकता (Conditional Probability)

P(B | A) = P(A ∩ B) / P(A)

6. बिनोमियल वितरण (Binomial Distribution)

P(X = r) = (nCr) × p^r × (1 − p)^(n − r)
जहां:
- n = कुल प्रयासों की संख्या
- r = सफल प्रयासों की संख्या
- p = सफलता की प्रायिकता
- nCr = संयोजन (Combination)

7. समीकरण (Expected Value)

E(X) = Σ [ x * P(x) ]

8. विविधता और मानक विचलन (Variance and Standard Deviation)

V(X) = Σ [ (x − E(X))^2 * P(x) ]
σ(X) = V(X)

9. कांबिनेशन और पर्मुटेशन (Combination and Permutation)

nPr = n! / (n − r)!
nCr = n! / [ r! (n − r)! ]

10. संभावना का सामान्यीकरण (Generalized Probability)

P(A1 ∪ A2 ∪ … ∪ An) = P(A1) + P(A2) + … + P(An) − P(A1 ∩ A2) − … − P(A(n-1) ∩ An) + P(A1 ∩ A2 ∩ … ∩ An)

11. मर्यादा और पूर्ति सिद्धांत (Law of Total Probability)

P(B) = Σ P(Ai) × P(B | Ai)
जहां Ai, सभी परस्पर बंटे हुए ईवेंट्स हैं

12. बेयस का थ्योरम (Bayes' Theorem)

P(A | B) = (P(B | A) × P(A)) / P(B)
यह शर्तीय प्रायिकता का एक रूप है जिसमें भविष्य की घटनाओं का अनुमान होता है।

13. निरंतर वितरण (Continuous Distribution)

फॉर्मूला: P(a ≤ X ≤ b) = ∫(a to b) f(x) dx
जहां f(x) निरंतर वितरण का प्रायिकता घनत्व फलन (PDF) है।

14. औसत या म्यू (Mean) (For Continuous Distribution)

μ = ∫(−∞ to ∞) x f(x) dx

15. पाई कोड के जरिए प्रायिकता (Probabilistic Modelling)

प्रायिकता का माप विभिन्न अनुप्रयोगों में किया जाता है, जैसे कि डेटा माइनिंग, रिस्क मैनेजमेंट, गेम थ्योरी में।